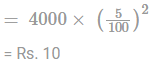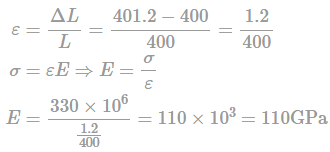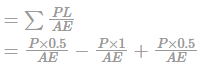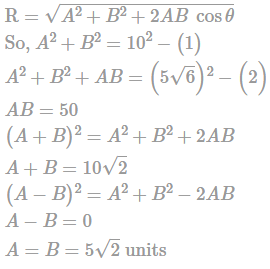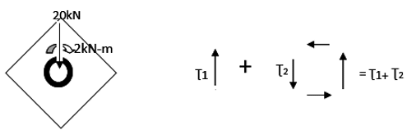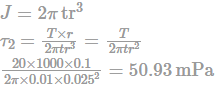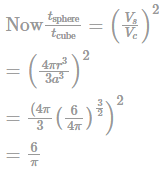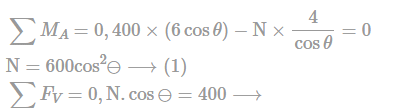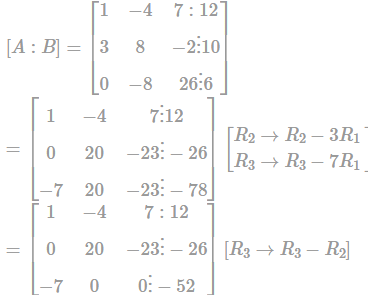Practice Test: Mechanical Engineering (ME)- 12
65 Questions MCQ Test GATE Mechanical (ME) 2023 Mock Test Series | Practice Test: Mechanical Engineering (ME)- 12
| 1 Crore+ students have signed up on EduRev. Have you? |
Mr. Rammurthy starts a business investing 250000 in year 1998. In year 1999 he invested an additional amount of 100000 and Mr. Siddharth Rau joined him with an amount of 350000. In year 2000. Mr. Rammurthy invested another additional amount of 100000 and Mr. Rajan Babu joined them with an amount of 350000. What will be Siddharth Rai’s share in the profit of 1500000 earned at the end of three years from the start of the business in 19988?
= (250000 × 3 + 100000 × 2 + 100000 × 1)
=1005000
Siddharth’s investment for 3 yr
= 350000 × 2 =700000
Ranhan’s investment for 3 yr
=350000 × 1 = 350000
Ratio = 1005000:700000:350000
= 3 :2 :1
Siddhartha’s profit
What is the difference between the compound interest and simple interest on Rs. 4000 at 5% per annum for 2 years?
In the following question, out of the five alternatives, select the word similar in meaning to the given word.
Sedition
Allegiance (n.): loyalty or commitment to a superior or to a group or cause.
Homage (n.): special honour or respect shown publicly.
Adulation (n.): excessive admiration or praise.
Allaying (v.): diminish or put at rest (fear, suspicion, or worry).
Insurrection (n.): a violent uprising against an authority or government.
So, the correct answer is option D.
Two pipes A and B can fill a tank in 36 min and 45 min respectively. A waste pipe C can empty the tank in 30 min. If all the pipes are opened together then the tank will be full in how much time?
Part filled by pipe B in 1 min = 1/45
∴ Total water dropped in the tank in 1 min = 1/36 + 1/45
Water leaked out in 1 min by C = 1/30
∴ Total tank filled in 1 min
Hence, the tank will be filled in 60 min.
Direction: In each question, a sentence with four words printed in bold are given. These are numbered as (1), (2), and (3). One of these four words printed in bold may be either wrongly spelt or inappropriate in the context of the sentence. Find out the word, if any, which is wrongly spelt or inappropriate. The number of that word is the answer. If all the words printed in bold are correctly spelt and appropriate in the context of the sentence, mark (4), i.e., 'All correct' as the answer.
No incidence of violence (1)/ occurred during the protests (2)/ against the Government’s (3)/ All correct (4)
In the following question, select the related word pair from the given alternatives.
? : Sun :: Rain : ?
Here the related word pairs are- (Light, Cloud)
Sun gives us light in same way Cloud gives us rain (so, Light : Sun :: Rain : Cloud).
Hence, option (B) is the correct response.
72% of the students of a certain class took Biology and 44% took Mathematics. If each student took at least one of Biology or Mathematics and 40 students took both of these subjects, the total number of students in the class is?
Percentage of students opting for both subjects
= 72 + 44 - 100 = 16%
If the total number of students be x, then
x = 4000/16 = 250
Study the following paragraph and answer the given questions.
Fashion has become one of the largest fads among the youth. The amount of time wastage and expenditure on fashion is very large. What bothes however is the fact that fashion is here to stay despite countless arguments against it. What is required therefore is that strong efforts should be made in order to displace excessive craze of fashion from the minds of today's youth.
Which of the following statements finds least support by the argument made by the author in the given paragraph?
Fashion usually is neither named nor noted but is simply the lens through which our society perceives itself and the mold to which it increasingly shapes itself. This hidden, powerful, mental sort of fashion is thus worth taking stock of. In spite of its great parade of intellect, its support in influential places, and its mellifluous accompaniment of self-promoting public relations, the new variety of fashion pretty much shares the creed and the limitations of the frivolous, pirouetting old variety of fashion—that of dress.
Option C is correct.
Direction: Find out the number of students who play only cricket.
Note : Total number of students - (25 +22) = 47
The number of students who play only cricket
= 25 - 16 = 9
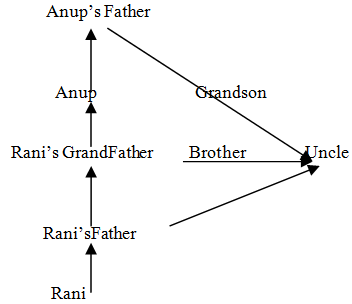
If the uncle of the father of Rani is the grandson of the father of Anup and Anup is the only son of his father, then what is the relation of Anup with Rani?
There are 3 lines (1 line for each generation) between Anup and Rani, So this is clear that Anup is the great grandfather of Rani.
A copper rod 400mm long is pulled in tension to a length of 401.2 mm by applying a tensile stress of 330 MPa. Then Young’s modulus of copper is
Lf = 401.2mm, Li = 400mm
σ = 330MPa
Find optimum order quantity where annual demand is 400 and ordering cost is 250 per order Carrying cost per unit 2%.
Which is in Range, this is order quantity.
Consider the following statements:
P: Casting yield is kept minimum while designing a gating system.
Q: Gating ratio of 4:1:1 corresponds to a pressurised gating system.
R: Possibility of air aspiration effect is more in unpressurised gating system
S: Pressurised gating system can only be used for non ferrous castings
Which of above statements are correct?
Pressurised gating system is used for ferrous castings
The general solution of the differential equation 
with C1 and C2 as constants are:
m = 2, 2
Complementary function = (C1 + C2x)e2x
Particular Integral
Put D = 2 (case fails)
(case fails)
General solution = C.F+P.I
A square bar with tapered length having circular cross section area having diameter 10 cm and 20 cm at two ends and length of the bar is 80 cm is subjected to a tensile force of 50 KN. If the bar is made up of steel having modulus of elasticity 200GPa, Find the elongation of the tapered bar (in mm) _______.
P = 50 kN,
L = 80cm,
D1 = 10cm
D2 = 20 cm
Elongation of tapered bar is given as
A stone is dropped from a balloon going up with a uniform velocity of 10 m/s. if the balloon was 40 m high when the stone was dropped, the height of balloon from the ground when the stone hits the ground is (take g = 10 m/s2)
Considering vertically downward as +ve and upward -ve.
S = ut+1/2gt2
S = 40m
u = −10m/s
40 = − 10t + 1/2 × 10 × t2
t2 − 2t − 8 = 0
t2 − 4t + 2t − 8 = 0
t = −2 (no significance in this problem)
t = 4s
Distance covered by balloon in 4 s in upward direction
= 10t = 40m
Total height of balloon = 40 + 40 = 80m
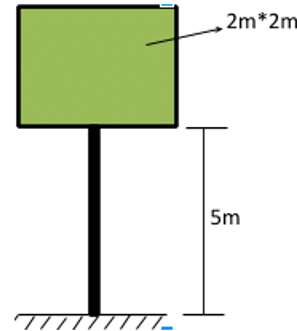
A banner hoarding having dimensions 2m × 2m is kept vertical by a 5m long pillar. Air blowing at 5 m/s is striking directly to the banner. If the maximum moment the pillar can withstand is 100 Nm. To reduce the drag force holes need to be cut out from the hoarding with a punch of 10 cm diameter. If the air drag coefficient is 0.5, then the total number of holes need to be cut out are
M= F × (5 + 1)
⇒ F= 100/6 = 16.67
That much amount of force can be applied by air, hence it should be equal to drag force,
F= 1/2 CDρAV2
16.67=1/2 (0.5)(1.2) × A × (5)2
A = 2.223 M2
The excess area need to cut from the hoarding
Area of hoarding – A
= 2 × 2 – 2.223
= 1.777 m2
Number of holds need to cut,
An double slider chain mechanism with the slotted link of length 5 units FIXED. A point on the link traces a curve which has a slope dy/dx = -2√3 eat the point (√3/2,1). Find the equation of the curve.
x2/a2 + y2/b2 = 1
Since the point (√3/2,1) lies on a curve, substituting in the above equation we get
(3/4a2) + (1/b2) = 1
Again differentiating we get 2x/a2 + 2y/b2dy/dx = 0
Putting point (x, y) = (√3/2,1) and dy/dx = -2√3
We get b2 = 4a2
Solving both we get a = 1,b = 2
The curve traced by a point on the link is 4x2 + y2 = 4
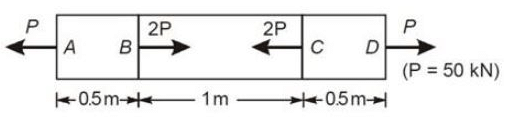
A slender bar of 100 mm2 cross-section is subjected to loading as shown in the figure. If the modulus of elasticity is taken as 200 × 109 Pa, then the elongation produced in the bar will be ____ mm.
= 0
The resultant of two vectors when acting at right angles is 10kN. If they act at 600 their resultant is 5√6 kN. Find the magnitude of individual vectors.
Two coins are tossed once, where E :no tail appears, F : no head appears. Find P(E/F).
i.e., E = {H H} and F = {T T}
⇒ E ∩ F = { } = ϕ
Hence, P (E ∩ F) = 0 and P(F) = 1/4
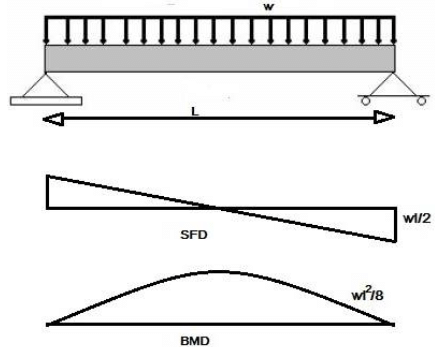
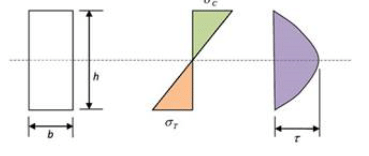
For a beam simply supported at ends, carrying UDL, the ratio of maximum principal stress at extreme fibre to maximum principal stress at neutral axis is___. The beam is square and length is 10 times the side of square.
Maximum stress on extreme fibre will be on point of maximum bending stress.
Max principal stress at N.A = τmaxNA
At point of maximum
A body is said to be provided optimum amount of streamlining when ______.
At a production machine, parts arrive according to a Poisson process at the rate of 0.35 parts per minute. Processing time for parts have exponential distribution with mean of 2 min. What is the probability that a random part arrival finds that there are already 8 parts in the system (in machine + in queue)?
λ = 0.35 per minute
µ = 1 /2 = 0.5 per minute
Hence,
ρ = λ/ µ = 0.7
The probability that a random part arrival finds that there are already 8 parts in the system is Pn = ρn (1−ρ) = 0.78 (1−0.7) = 0.01729
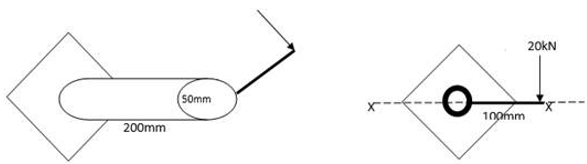
A Circular beam, 50 mm in diameter, is welded to the support by means of circumferential fillet weld as shown in the diagram. It is subjected to a eccentric load of 20kN at a distance of 100mm parallel to support and at distance of 200mm away from the support. Thickness of the weld is 10mm. Find Maximum principal stress at weld on X-X plane.
Primary shear will act upward
Secondary shear will act anti-clockwise so right side of the section equivalent shear will be the summation of primary and secondary shear.
The polar moment of Inertia of circular beam
As at X-X plane, there will not be any bending stress
So max principal stress = T1 + T2 = 63.66 MPa
The turbine rotor of a ship has a mass of 5000 kg and its radius of gyration is 500 mm. The turbine rotor rotates at 1500 rpm in counter-clockwise direction (view from stern or rear end). If the ship travels at a speed of 90 km/h and steer to the left in a curve of 100 m then the gyroscopic couple on the ship and its effect respectively are
km/h = 25m/s,R = 100m
The gyroscopic couple, C = IωωP
I = mk2 = 5000 × 0.52 = 1250kg − m2
ωp = ∨/R = 25/100 = 0.25m/s
C = 1250 × 157.08 × 0.25 = 49087.5N − m = 49.0875
kN−m
As rotor rotates in anticlockwise direction, when view from rear end and steering is towards left, so, the effect of gyroscopic couple will be to lower the bow and raise the stern end.
Consider following statements:
I) A gas is said to be an ideal gas when intermolecular forces are zero.
II) A gas behaves as an ideal gas under high temperature and high pressure.
III For an ideal gas, the temperature variation w. r. t. pressure during throttling condition is zero.
IV) A gas cools during expansion only when the Joule Thomson coefficient is negative.
Which of the following statements is/are correct?
Two castings of the same metal have the same surface area. One castings is in the form of a sphere and the other is a cube. What is the ratio of the solidification time for the sphere to that of the cube?
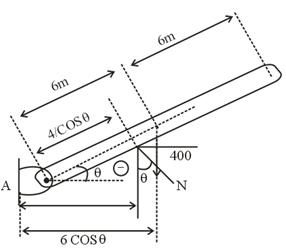
The uniform rod in figure weighs 400 N, length of the rod is 12 m
Determine the angle ɵ in degrees.
Fram 1 & 2
cos3 θ = 2/3
θ = 29.12
The system of equations x - 4y + 7z = 12 , 3x + 8y - 2z = 10, 26 z - 8y = 6
Here, Rank [A:B] = Rank[A] = 3 = n
And n = 3
Therefore, the system has unique solution.
A bar of length 2.1m and diameter 38mm is subjected to pure torsion. If the shear modulus of the material is 41GPa, calculate the torsional stiffness of the bar.
So, Torsional stiffness = 3996.67Nm
Two shafts of same material and same length are connected in series and subjected to a torque of 20 kN-m. If the ratio of their diameters is 1:3 then the ratio of their angles of twist is:
θ = TL/GJ
Where:
J = Polar moment of Inertia
The temperature of two thermometers A and B are tA and tB. The reading t a and tB agree at the ice point and steam point and are related as 
Where, a,b and c are constants and tA and tB are in ∘C The thermometers A and B, bath are immersed in a fluid and reads 45∘C
and 47∘C respectively. The thermometer reading A, when the thermometer B reads 22∘C
At ice point, tA = tB = 0∘C
a = 0
At steam point, tA = tB = 100∘C
100 = 0 + b × 100 + c × 1002
b + 100c = 1(11)
At tA = 45, tB = 47
45 = 0 + b × 47 + c × 472
b + 47c = 0.957 (iii)
Solving equation (ii) and (iii)
b = 0.919
c = 8.11 × 10−4
So, finally eq" (i) becomes
At tB = 22,
tA = 0.919 × 22 + 8.11 × 10-4 × 222 = 20.61°C
A shaft compressed all round by a hub will have a Mohr’s circle as __________.
Steam flows at the rate of 5m3/s at a particular section in a reaction turbine where the diameter of blade is 2m and the velocity of flow is 6m/s. What is the blade height of section _________mm.
Q = A × V
5 = πdh × Vf
A conical valve of weight 3 kN is used to stop the flow of water from bottom the tank as shown in the figure. Find the force F (in kN) required to stop the flow of water from the bottom of the tank.
Now the radius of the cone is , r = 1 × tan 300 = 0.577 m
Fv = Fv1 + Fv2 = (πr2 * 2 – πr2*1/3) ρg
Fv = 17.12 kN
Fv + 3 = F
F = 17.12 + 3 = 20.12 kN
Far the Froude model law 1/25 model of a pipe is to be tested. If the discharge is 300m3/s, then the discharge at which the model must be tested is ……….m3/s?
The pressure on the fluid is 3 MPa. The Young’s modulus is 210 GPa and the Poisson’s ratio is 0.25, the volumetric compressive strain produced is
Given- P = 3MPa
E = 210 x 103 MPa
μ = 0.25
E = 3K(1 - 2μ)
εy = 21.42 x 10-6
If there are two materials A & B, for material “A”, Young’s modulus is twice the Shear modulus & for “B” Young’s modulus is thrice the bulk modulus, then μA & μB respectively are
For A
E = 2G(1 + μ)
For B
E = 3K(1 − 2μ)
E = 2G for "A",μA = 0
E = 3K for "B",μB = 0
Consider a stepped shaft subjected to a twisting moment applied at B & C as shown in the figure. Assume shear modulus, G = 80 GPa. The angle of twist at D (in degrees) is ______ (corrected up to 3 decimal places)
Tatal twist at C will be equal ta D
θe = θAB + θBC = θD
θD = 0.00673 radian
= 0.386 degree
In an epicyclic gear train, an arm carries two gears A and B having 36 and 45 teeth respectively. If the arm rotates at 150 r.p. m. in the anticlockwise direction about the centre of the gear A which is fixed, determine the speed of gear B. If the gear A instead of being fixed, makes 300 r.p.m. in the clockwise direction, what will be the speed of gear B?
Let
NA = Speed of gear A
NB = Speed of gear B, and
NC = Speed of arm C
Assuming the arm C to be fixed, speed of gear A relative to arm C
= NA − NC
and speed of gear B relative to arm
C = NB − NC
since the gears A and B revolve in opposite directions, therefore
Speed of gear B when gear A is fixed
When gear A is fixed, the arm rotates at 150 r.p.m. in the anticlockwise direction, i.e.
NA = 0, and NC = +150r⋅p⋅m
or NB = −150 × −0.8 + 150 = 120 + 150 = 270r⋅p⋅m⋅ Ans.
Speed of gear B when gear A makes 300 r.p.m. clockwise
since the gear A makes 300 r.p.m. clockwise, therefore
NA = −300r⋅p⋅m
NB = -450 x -0.8 + 150 = 360 + 150 = 510 r.pm. Ans
The cost parameters and other factor for a production inventory system of automobile factory are
Demand / year = 6000 units
Unit cost = Rs. 40/-
Setup cost (order cost) = Rs. 500/ set up
Production rate/ year = 36000 units
Holding cost/unit/year = Rs. 8/-
Shortage cost/unit/year = Rs. 20/-
The optimal lot size would be _____ units.
D = 6000 units
C0 = Rs. 500, P = 36000 units
Cn = Rs. 8, Cb = Rs. 20
= 1122.49 = 1123units
The number of degrees of freedom for the mechanism shown will be.
The mechanism consists a cam pair. Therefore, its degree of freedom must be found from Grubler’s criterion.
F = 3(l-1)-2j-h
l→ Number of links
j→ Number of binary points
h→ Number of higher pairs
here, l = 7
j = 8
h = 1
F = 3(7 - 1) -2 × 8 - 1
F = 1
A laminar fully developed fluid (k = 0.175 W/m-K) flow inside a 6 mm internal diameter tube under uniform wall temperature boundary conditions. Compute the heat transfer rate between the tube walls and the fluid for a length of 8 m if the mean temperature difference between the wall and the fluid is 50 °C.
Nu = kD/k = 3.66
(for fully developed laminar flow under
uniform wall temperature condition)
or
= 106.75 W/m2-K
Now, Q = h(πDL)∆T
= (106.75)(π × 0.006 × 8) × 50
= 804.87 W
Since the function has 0/0 from now, we can apply L’ Hopital rule,
Applying limit now,
A grinding operation requires 5 kW of power to be carried by the motor. The material removal rate is given as 23.65 mm3/sec and the grinding ratio is given as 12. Find the wear rate of the grinding grains of the grinding wheel.
We know that
=1.97 mm3/sec.
In the figure shown, the input M has a 48 teeth, B and D constitute a compound planet having 60 and 36 teeth respectively.
If all the gears are of same pitch, find the ratio of speeds of gear M to gear L, assuming N to be fixed.
TM = 48 teeth
TB = 60 teeth
TD = 36 teeth
Pitch diameters of wheels are proportional to the number of teeth on them.
TN = TM + 2TB = 168 teeth
TL = TM + TB + TD
TL = 144 teeth
From the given condition
A large turbine generates a power of 1000 kW under a head of 50 m. A 1/5th model of a hydraulic turbine is tested against a head of 10 m. The power developed (kW) and the discharge flow rate (m3/s) by the model are
Given
Pp = 1000 kW
Hp = 50 m
Pp = ρgQpHp
We know that head coefficient,
and the power coefficient
and distance flow rate, Qm
Pm = ρgQmHm
Two streams of fluids of unit constant specific heat and unit mass flow rate exchange thermal energy in an adiabatic heat exchanger. The inlet temperature of hot and cold fluid streams is 300 0C and 30 0C respectively. The effectiveness of the heat exchanger if the outlet temperature of both the fluid are equal is
For zero entropy condition, outer temperature of both the fluid must be same,
Hence, mhCh (300-t) = mhCh (t-30)
t = 105° C
And this condition is possible only in case of counter flow heat exchanger.
Oil of viscosity 0.085 Ns/m2 is filled between two 120 cm long concentric cylinders having inner and outer radius as 5cm and 6cm. If the inner cylinder is fixed and outer cylinder, I rotate at 900 rpm. If the inner cylinder is also rotating at 500 rpm in the same direction as that of outer cylinder. Then percentage reduction in shear stress is
We know that shear stress is given by
When inner cylinder is fixed.
= 2883.98N/m2
When outer cylinder is rotated at 500 rpm in same direction,
the net rotation of outer cylinder = 900 – 500
= 400 rpm
=1281.769N/m2
% age change in shear stress
= 55.56%
The following table shows the unit cost of transportation associated from ith source to jth destination. The demand and supply at different location are also given in table. The initial basic feasible solution using Vogel’s approximation method is
Total demand = 3 + 4 + 6 + 7 + 10 = 30
Total supply = 5+13+12 = 30
As, Total supply = Total demand, i.e., problem is balanced
No. of filled cell = 7
The required no. of cell = m + n - 1 = 5 + 4 - 1 = 8
If, No. of filled cell < required="" no.="" of="" cell="" degenerate="" />
If, No. of filled cell = required no. of cell non degenerate solution
IIf, No. of filled cell > required no. of cell redundant solution
As, no. of filled cell < required="" no.="" of="" cell,="" so="" the="" solution="" is="" degenerate="" and="" the="" corresponding="" transportation="" cost="" is="" given="" />
Total transportation cost = 2×4 + 2×1 + 2×3 + 6×3 + 4×6 + 7×3 +10×1 = 89
Five jobs are to be assigned at a particular firm. Their work (processing) time and due dates are given in the following table. If the sequence of processing is according to earliest due date (EDD) then the average no. of jobs in the system is
Average no. of jobs in system
The principal stresses at a point inside a solid object are σ1 = 100 MPa, σ2 = 100 MPa and σ3 = 0MPa. The yield strength of the material is 200 MPa. The factor of safety calculated using Tresca theory is nT and the factor of safety calculated using Von-Mises theory is nV. Which one of the following relations is TRUE?
Given that, σ1 = 100Mpa, σ2 = 100Mpa
σ3 = 0,σy = 200Mpa
Naw, maximum shear stress is given by
Hence, Tmax = 50Mpa.
Applying Tress's theory
⇒ FosT = 2
⇒ nT = 2……(1)
Applying Yon-mises theory.
Using N = nt
and salving using the given values, we get nt = 2
Sa nv = nt = 2
The inner and outer diameters of a multiple plate clutch disc are 100 mm and 200 mm respectively. The friction coefficient and permissible intensity of pressure is 0.2 and 1 MPa. The no. of pair of contacting surfaces if the torque carrying capacity of clutch at 750 rpm is 1.1 KN-m (assume uniform pressure theory)
Where, Z= No. of pair of contacting surfaces μ = 0.2
P = Operating farce p = 1MPa
r = 100/2 = 50mm
R = 200/2 = 100mm
Rm = mean radius
For uniform pressure theory
Far uniform wear theory
P = 7T [R2 - r2] x p = π [1002 - 502] x 1
P = 23561.95N
M t = Z x 0.2 x 23561.95 x 77.77N - m m = 0.366 x ZKN - m
1.1 = 0.366 x Z
Z = 3
A close-coiled helical spring, made out of a 10 mm diameter steel wire, has 20 complete coils each of mean diameter of 100 mm. A weight of 10 kg is dropped onto the spring, compresses it 60 mm, then height from which the weight is dropped (in mm) will be (take G = 85000 MPa)
Now, by energy balance
⇒ h = 37.48mm
In a machining experiment, the tool life was found to vary with cutting speed in following manner
If tool changing time is 3 minutes, then the optimum value of cutting speed (in m/min) for maximum productivity is
Using Taylar's taal life equation,
VTn = C
100 × 10n = C…….(1)
75 × 30n = C………
From equation (1) and (2) , we get
n = 0.2616 and C = 182.6
Now applying the maximum productivity criteria
A sprue with gate diameter of 5 cm is used to fill a 80 cm diameter and 50 cm high cylindrical casting. If the head available for filling metal is 75 cm, then the minimum time taken in seconds to fill up the casting is
Top gating always takes less time than bottom gating. So, the minimum filling time will be in top gating.
Velocity at gate, 
Then time taken to fill the cavity is given by
In a wire drawing operation the 12 mm dia. wire is reduce to 8 mm. Mean flow stress is taken 500 MPa, drawing load and stress required for wire drawing operation respectively.
P = 20.378KN
Drawing stress:
A shaft has a dimension of 
the respective values of upper deviation, lower deviation and mean deviation.
0.04,-0.02,0.01 upper deviation = max. size − basic size
= 20.04 − 20 = +0.04
Lawer deviation = min size - basic size
= 19.98 − 20 = −0.02
Mean deviation 
A CNC part programming on a block is given by
M020 G02 X45.0 Y25.0 R5.0
The tool motion during the execution of the part programme will be
Given:- MO20 GO2 X45.0 Y25.0 R5.0
Here term ×45.0Y25.0R5.0 will produce circular motion
because radius is consider in this term and GO2 will
produce clockwise motion of the tool.
Three masses m1, m2 and m3 of magnitude 50 kg, 100 kg and 200 kg are connected to a rotating shaft. The corresponding radiuses of rotation are 0.4 m; 0.2 m and 0.1 m respectively and angle between successive masses are 60 and 150. What is the magnitude of balancing mass if its radius of rotation is 0.3 m?
m1 = 50kg,m2 = 100kg,m3 = 200kg
The horizontal component of centrifugal farce ∑H =
[50 × 0.4 + 100 × 0.2 × cos60∘ + 200 × 0.1 × cos 210∘]ω2
= 12.68ω2
The vertical component of centrifugal farce ∑V = [100 × 0.2 × sin60∘ + 200 × 0.1 × sin 210∘]ω2 = 7.32
ω2
The resultant force, 
ω= angular velocity of rotating masses. Suppose the balancing mass M acting moving with angular velocity ω at a radius of rotation 0.3m and it is given as
M × 0.3 × ω2 = 14.64ω2
M = 48.8kg
The angle made by resultant with horizontal force anticlockwise, is given as
The location of M = 180∘ + 30∘ = 210∘ ta the anticlockwise of 200 kg mass
A mass M, of 20 kg is attached to the free end of a steel cantilever beam of length 1000 mm having a cross-section of 25 × 25 mm. Assume the mass of the cantilever to be negligible and Esteel = 200GPa. If the lateral vibration of this system is critically damped using a viscous damper, the damping constant of the damper is
Given M = 20kg,I = 1000mm = 1m, A = 25 × 25
mm2
ESteel = 200GPa = 200 × 109Pa
Mass moment of inertia of a square section is given by,
Deflection of a cantilever, Loaded with a point load placed at the free end is
Therefore, critical damping constant C0 = 2Mωn = 2 × 20 × 31.32
= 1252.8Ns/m ≃ 1250Ns/m
In aqua- ammonia absorption refrigeration system, the temperature to be maintained in the refrigerator is −5∘C and the ambient temperature is 27∘C. If the actual COP is 50% af the maximum COP and the heat supply to generator is 120KW at 110∘C, then the refrigeration load is
given, QG = 120KW
Generator temperature, T1 = 110∘C + 273 = 383K
Condenser and absorber temperature, T2 = 27 + 273 = 300K Evaporator temperature,
TR = -5°C + 273 = 268K
(COP)max = product of ideal COP of a refrigerator warking between TR and T2 and ideal thermal efficiency of an engine working between T1 and T2
= 1.81
(COP)actual = 0.5 X 1.81 = 0.9
Refrigeration load, QE = 108KW
In an ideal Brayton cycle with regeneration, air is compressed from 1 bar and 300 K to 4 bar and 450 K, is heated to 750 K in the regenerator, and then further heated to 1200 K before entering the turbine. Under cold-air standard conditions, the effectiveness of the regenerator (in percentage) is _____ [Take γ = 1.3 for gas]
Given, P1 = 1 bax = P4
P2 = 4 bar = P3
T1 = 300K
T2 = 450K
T6 = 750K
T3 = 1200K
A 4-stroke and 8 cylinder gas engine with a stroke volume of 2 litre develops 30 KW at 510 rpm. The indicated mean effective pressure is 600 KN/m2. The average no. of times each cylinder misfired in one minute is
Given,
Vs = 2 litre = 0.002m3
Indicated mean effective pressure (imep) = 600 KN/m2 N = 380rpm
Indicated power per cylinder 
n = no. of explosion per minute No .of explosions per minute = N/2 = 510/2 = 255 No. of misfiring per minute per cylinder = 255 − 250 = 5
|
26 docs|239 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
26 docs|239 tests
|
Download free EduRev App
Related content with Practice Test: Mechanical Engineering (ME)- 12
|
|
Related tests with Practice Test: Mechanical Engineering (ME)- 12
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
