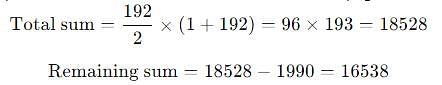Practice Test: Number System- 2 - CAT MCQ
20 Questions MCQ Test Quantitative Aptitude (Quant) - Practice Test: Number System- 2
The HCF of two numbers is 11 and their LCM is 616. If one of the numbers is 77, find the other number.
Let a, b, m and n be natural numbers such that a > 1 and b > 1. If ambn = 144145, then the largest possible value of n - m is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A shop stores x kg of rice. The first customer buys half this amount plus half a kg of rice. The second customer buys half the remaining amount plus half a kg of rice. Then the third customer also buys half the remaining amount plus half a kg of rice. Thereafter, no rice is left in the shop. Which of the following best describes the value of x?
Let N = 1421 * 1423 * 1425. What is the remainder when N is divided by 12?
How many divisors of 105 will have at least one zero at its end?
Tatto bought a notebook containing 96 pages leaves and numbered them which came to 192 pages. Tappo tore out the latter 25 leaves of the notebook and added the 50 numbers she found on those pages. Which of the following is not true?
There are 50 integers a1, a2,........, a50, not all of them necessarily different. Let the greatest integer of these 50 integers be referred to as G, and the smallest integer is referred to as L. The integers a1 through a24 form sequence S1, and the rest form sequence S2. Each member of S1 is less than or equal to each member of S2.
Every element of S1 is made greater than or equal to every element of S2 by adding to each element of S1 an integer x. Then, x cannot be less than:
Srini wrote his class 10th board examination this year. When the result came out he searched for his hall ticket to see his roll number but could not trace it. He could remember only the first three digits of the 6 digit number as 267. His father, however, remembered that the number was divisible by 11. His mother gave the information that the number was also divisible by 13. They tried to recollect the number when all of a sudden Srini told that the number was a multiple of 7. What was the unit digits of the number?
When 7179 and 9699 are divided by another natural number N , remainder obtained is same. How many values of N will be ending with one or more than one zeroes?
At a bookstore, 'MODERN BOOK STORE' is flashed using neon lights. The words are individually flashed at the
intervals of 2.5 s, 4.25 s and 5.125 s respectively, and each word is put off after a second. The least time after
which the full name of the bookstore can be read again for a full second is
Find the remainder when 73 * 75 * 78 * 57 * 197 * 37 is divided by 34.
Three distinct prime numbers, less than 10 are taken and all the numbers that can be formed by arranging all the digits are taken. Now, difference between the largest and the smallest number formed is equal to 495. It is also given that sum of the digits is more than 13. What is the product of the numbers?
Which of the following would always divide a six-digit number of the form ababab?
When a number is successively divided by 7,5 and 4, it leaves remainders of 4,2 and 3 respectively. What will be the respective remainders when the smallest such number is successively divided by 8,5 and 6 ?
Four bells ringing together and ring at an interval of 12 sec, 15 sec, 20 sec, and 30 sec respectively. How many times will they ring together in 8 hours?
What would be the greatest number that divides 14, 20, and 32 leaving the same remainder?
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|