Practice Test: Quantitative Aptitude - 4 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2024 - Practice Test: Quantitative Aptitude - 4
The length of a rectangle is 2 cm more than its breadth. The diagonal is 5 cm. Find the length of the rectangle?
The wheel of a railway carriage is 3 m in diameter and makes 8 revolutions per second, how fast is the train going?a. 27
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A wholesaler marks his goods 35% above the cost price. If he allows a discount of 6 1/5%, then his profit percent is
A sum of Rs. 25220 is borrowed at 5% per annum compounded annually which is paid back in 3 equal instalments. What is the amount of each instalment?
The average monthly income of A and B is Rs. 5000. The average monthly income of B and C is Rs. 7250 and the average monthly income of A and C is Rs. 8500. Find the monthly income of A ?
An good is sold at a certain price. By selling it at ¾ of that price one loses 20%. Find the profit percent at its original price.
In an examination, 30% of total students failed in Hindi, 25% failed in English and 10% failed in both. Find the percentage of those students who passed in both the subjects?
Shiva travelled from home to temple at the rate of 35 kmph and returned at the rate of 6 kmph. If the whole journey took 4 hours 45 minutes. Find the distance between home and temple.
Find the value of x in the following expression 2x - 3 = 1/(8x - 4)
If (4y + 72), (33 + y) are supplementary angles, find y?
One angle of a triangle is 60° and other angle is π/2 radian. Find the third angle in centesimal unit?
A can work twice as B and they together can finish a work in 16 days. In how many days will A alone finish the work?
If a + b = 26 and a - b = 9 then the value of (4a2b2) is,
If x + y = √3 and x - y = √2, then the value of (x2 + y2) is
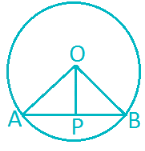
If the length of a chord is 24 cm which is at a certain distance from the centre of a circle of radius 13cm. Find distance between chord from centre of the circle?
Each interior angle of a regular polygon is 150°. The number of sides is
If 2sin2θ + 4 cos2θ = 3, then find the value of θ ?
A sum of amount at r% compound interest doubles in 3 years. In 6 years it will be k times of the original principle. What is the value of k?
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 45°, when retreats 50 m from the bank he finds the angle to be 30°. find the height of the tree and breadth of the river ?
The following diagram shows the percentages of different grades of the 20000 students in the college. Observe the pie diagram and answer the questions
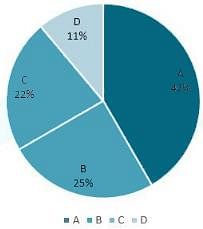
Question: Find the number of students who got A grade?
The following diagram shows the percentages of different grades of the 20000 students in the college. Observe the pie diagram and answer the questions

Question:Find the ratio between the number of students who got A grade and B grade?
The following diagram shows the percentages of different grades of the 20000 students in the college. Observe the pie diagram and answer the questions
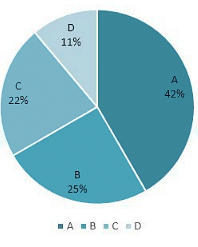
Question: Find the ratio between number of students who got C grade and D grade?
The following diagram shows the percentages of different grades of the 20000 students in the college. Observe the pie diagram and answer the questions

Question: Find the ratio between difference of number of students who got A and B grades to the difference of the number of students who got C and D grades?
|
237 docs|133 tests
|
|
237 docs|133 tests
|



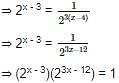
 then the value of x is
then the value of x is