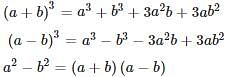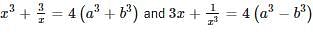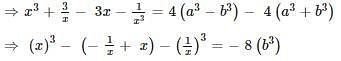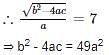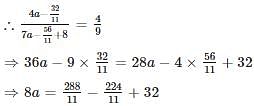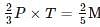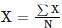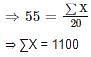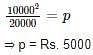Practice Test: Quantitative Aptitude - 6 - SSC CGL MCQ
25 Questions MCQ Test SSC CGL Tier 1 Mock Test Series 2024 - Practice Test: Quantitative Aptitude - 6
Directions: The pie chart given below represents the modes of transport for 1400 employees of the staff Selection Commission, Kolkata. Study the chart and answer the questions.
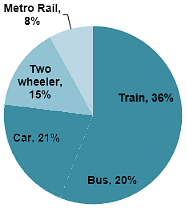
Question: The number of employees who go to office by Metro Rail is
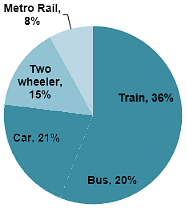
Question: The number of employees who go to office by Metro Rail is
Directions: The pie chart given below represents the modes of transport for 1400 employees of the staff Selection Commission, Kolkata. Study the chart and answer the questions.
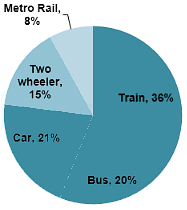
Question: The number of employees who go to office by car is
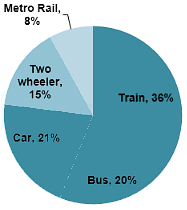
Question: The number of employees who go to office by car is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Directions: The pie chart given below represents the modes of transport for 1400 employees of the staff Selection Commission, Kolkata. Study the chart and answer the questions.

Question: The ratio of two wheelers and cars being used as modes of transport is

Question: The ratio of two wheelers and cars being used as modes of transport is
Directions: The pie chart given below represents the modes of transport for 1400 employees of the staff Selection Commission, Kolkata. Study the chart and answer the questions.
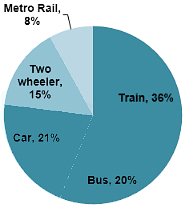
Question: Write down the difference: (Employees availing train - employees availing car)
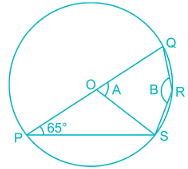
O is the center of circle and ∠QPS = 65°. Find the value of ∠A and ∠B respectively.
Find the third vertex of a triangle, if two of its vertices are at (2, 3) and (4, -2) and the centroid is at (1, 1).
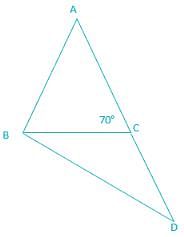
The side AC of the ΔABC is produced to D, such that CD = CB. If ∠ACB = 70°, then the value of ∠ADB is
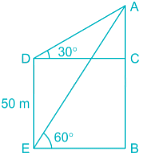
The angles of depression of the top and bottom of a 50 m high electric pole form the top of a building are 30° and 60° respectively. Find the height of the building.
The simplest value of cot9° cot27° cot63° cot 81° is
ABC is an equilateral triangle with side 2 cm. With A, B and C as centres and radius 1 cm three arcs are drawn. The area of the region with in the triangle bounded by three arcs is
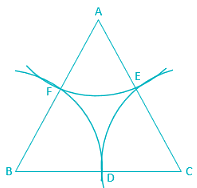
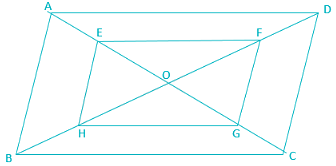
ABCD is a parallelogram in which diagonals AC and BD intersect at O. If E, F, G and H are the mid points of AO, DO, CO and BO respectively, then the ratio of the perimeter of the quadrilateral EFGH to the perimeter of parallelogram ABCD is
If the roots of the equation ax2 + bx + c = 0 differ by 7, then which of the following expression shows the relation among a, b and c?
A can do a piece of work in 18 days, B in 36 days and C in 72 days. All begin to do it together but A leaves after 8 days and B leaves 7 days before the completion of the work. The total number of days they worked for is
Form two places, 60 km apart, A and B start towards each other and meet after 6 hours. Had A travelled with 2/3 of his speed and B travelled with double of his speed, they would have met after 5 hours. The speed of A is:
A container contains mixture of milk and water in the ratio of 4 : 7. 8 litres of this mixture is replaced by water. The new ratio of milk and water becomes 4 : 9. Find the initial quantity of water in the mixture.
Ram and Shyam start a joint business. Ram invests 1/3 of the total sum for 9 month and Shyam gets 2/5 of the profits. For how long, the investment of Shyam was in the business?
The mean of 20 items is 55. If two items 45 and 30 are removed, the new mean of the remaining items is
The percentage of metals in a mine of lead ore is 60%. Now the percentage of silver is 3/4 % of metals and the rest is lead. If the mass of ore extracted from this mine is 8000 kg, then the mass (in kg) of lead is:
A sum becomes Rs, 10000 after 3 years and Rs, 20000 after 6 years on compound interest. The sum is
The ratio of monthly incomes of A and B is 7: 8 and their monthly expenditures in ratio of 3: 4. If each of them saves Rs. 400 per month. Find the sum of their monthly income.
For any integral of n, 32n + 9n + 5 when divided by 3 will leave the remainder
|
237 docs|133 tests
|
|
237 docs|133 tests
|


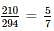
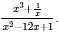
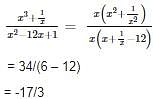

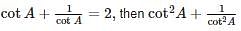 is equal to
is equal to
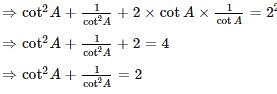
 then a2 – b2 is equal to
then a2 – b2 is equal to