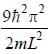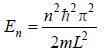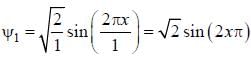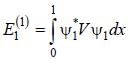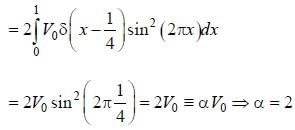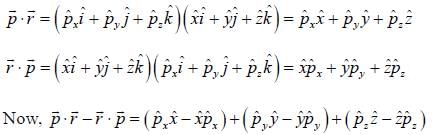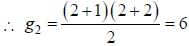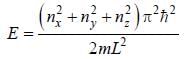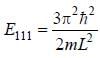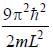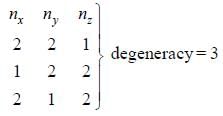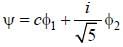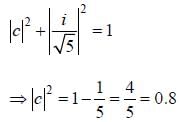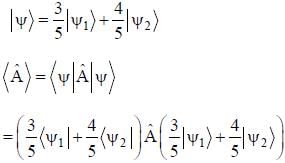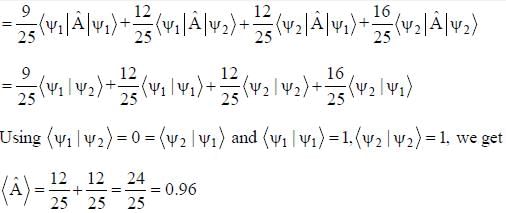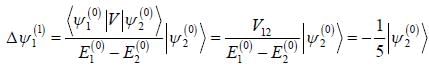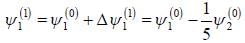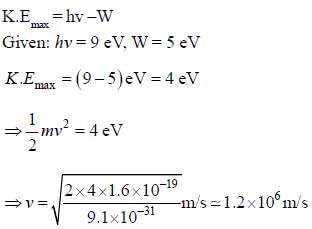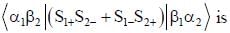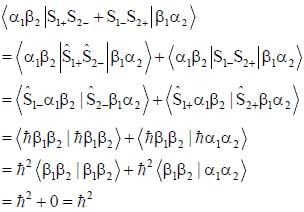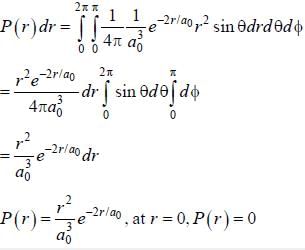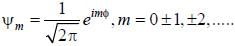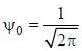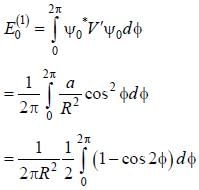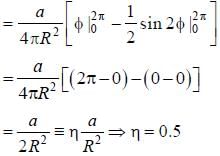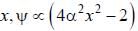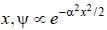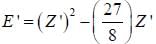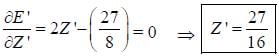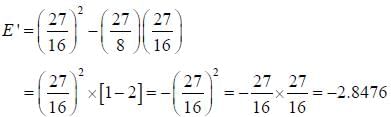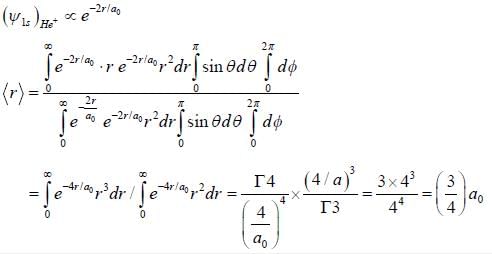Quantum Chemistry - 2
20 Questions MCQ Test GATE Chemistry Mock Test Series | Quantum Chemistry - 2
| 1 Crore+ students have signed up on EduRev. Have you? |
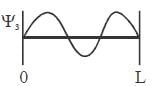
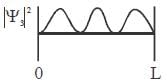
For the energy level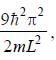 
the probability density for a particle of mass m is a one dimensional potential box of width L is given by
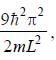the probability density for a particle of mass m is a one dimensional potential box of width L is given byGiven energy level E = 
So, the given energy level corresponds to n = 3
No, of nodes in ψ3 = 3 - 1 = 2
Probabilty density 
π-boncl length between C-C atoms. f.i and v is calculated by using the empirical formula,
Rμv = 1.52Å - 0.186 Å Pμv
where Pμv= is π - bond order between μ and v C -atom .
According to HM O theory. delocalization energy o f Benzene is 2|β|. Then T-bond length in Benzene is
Rμv = 1.52Å - 0.186 Å Pμv
where Pμv= is π - bond order between μ and v C -atom .
According to HM O theory. delocalization energy o f Benzene is 2|β|. Then T-bond length in Benzene is
Since, delocalization energy = 2|β|
So, one extra delocalizedT-bond Benzene.
The total energy of π-bond = 4(According to HMO Theory)
Since, there are 6(C- C ) bond in benzene.
So. each (C-C) bond has 4/6 π-bond = 2/s = 0.66
Now. by using formula,
Rμv = 1.52Å - 0.186 Å x 0.66 = 1.39 Å
According to Huckel molecular orbital theory, the total energy of hypothetical localized Benzene (C6H6) molecule is
So, there are three localized tt-bond. Ech have energy = 2α+ 2β
So, total localized energy= 3(2α + 2β) = 6α +6β
A perturbation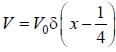 
is introduced in a box of width 1 unit, where V0 is ( << 1 ) is a positive constant. The first order energy correction to the first exited state is α V0 . The value of α is_________
First excited state wavefimction
First order eneigy correction to the first excited state is
σx , σy and σz are the Pauli m atrices. The expression is equal to 2σx σy + σy σx is equal to
2σx σy + σy σx
= σx σy + x σy + σy σx
= σx σy, as σx σy + σy σx = 0
= iσz
For linear momentum vector operator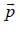 
-and position vector operator 
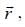the operator 
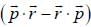is equivalent to
The degeneracy of the n = 2 level for a three dimensional isotropic oscillator is ________. (an integer)
Degeneracy for a three dimensional isotropic oscillator gn = 
n= 2
The operation of the commutator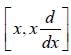 
on a function f ( x ) is equal to
The degeneracy of a quantum particle in a cubic box having energy three times that of the lowest energy is ________
Energy eigenvalue of a particle in a cubic box.
Groimd state energy corresponds to nx = ny = nz = 1
Three times the ground state energy = 
Consider a normalized molecular orbital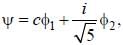 
constructed from two different atomic orbitals 
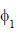and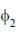 
that fonn an orthonormal set. Here i = √-1. The value of |c|2 is ______ (upto one decim al place)
Given: 
Nonnalization condition:
The normalized wavefiinctions ψ1 and ψ2 correspond to the ground state and the first excited states of a particle in a potential. The operator A acts on the wavefiinctions as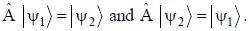 
The expectation value of the operator A for the state 
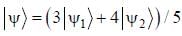is ________. (upto two decimal places)
Three identical non- interacting particles, each of spin 1/2 and mass m. are moving in a one-dimensional infinite potential well given by
the energy of the lowest energy state of the system is:
Figure shows the configuration of the lowest energy state of the system
A certain 2-level system lias stationary state energy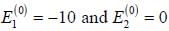 
with normalized wave functions
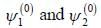respectively. A small perturbation V is applied on the system such that V12 = 2. The wavefunction of the particle in groimd state collected upto first order, will be
Fii'st order collection in the ground state wave function,
Collected ground state wave function,
Given that work function of a metal is 5 eV and that photons of 9 eV are incident on it. the maximum velocity of emitted electrons is approximately______ x106 m/s (upto one decimal place)
Maximum kinetic energy o qf the electrons,
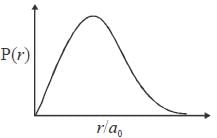
The ground state wave function of hydrogen atom is given by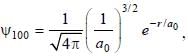 
where a0 is the Bohr
radius. The plot of the radial probability density P(r) for the hydrogen atom in the ground state is
The radial probability density is given by
Only option (d) satisfies this condition.
A particle of mass m is constrained to move in a circular ring of radius R . When a perturbation
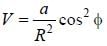
(where a is a real constant) is added, the first order collection to the ground state energy is 
The value
of η is ______ (up to one decimal place)
Wavefiinction for a particle in a circular ring of radius R is given by
Ground state wave function corresponds to m = 0, 
First order collection to ground state energy
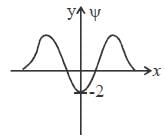
The wavefiuiction for a linear harmonic oscillator described by N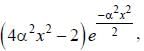 
where α and N are constants, has
For small values of 
For large values of 
The wavefunction will cut y-axis aty = -2.
ψ is even function. so it is symetric about y-axis.
From the graph, there are two maxima and one minimum only.
The ‘‘trial'’ wavefuction for He atom is taken as 
where N is the normalization factor and Z ' is the variational parameter. Expression for the energy in terms of Z ' is found to be
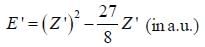
Then the lowest value of the energy ( E ') for He atom i s _________________(in a.u .)
(Round off to two decimal places)
For minimmn energy,
The minimum energy will be
The average distance between the electron and nucleus of a He+ (singly ionised Heliumion) in the 1s state is
|
1 docs|34 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
1 docs|34 tests
|
Download free EduRev App
Related content with Quantum Chemistry - 2
|
|
|
|
Related tests with Quantum Chemistry - 2
|
|
|
|
|
|
© EduRev
|
Follow Us
|