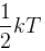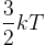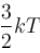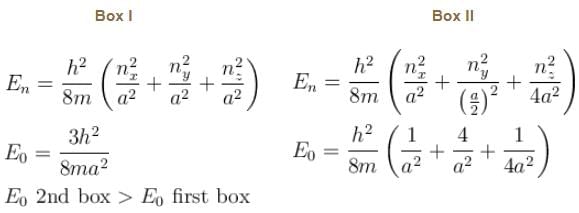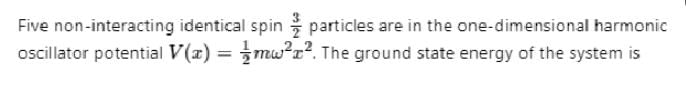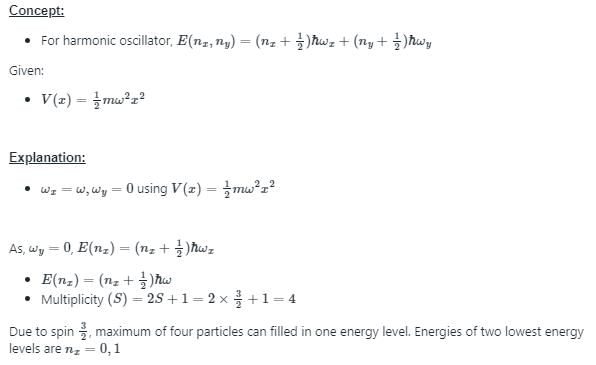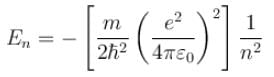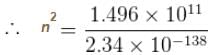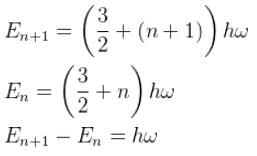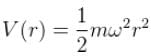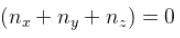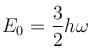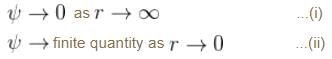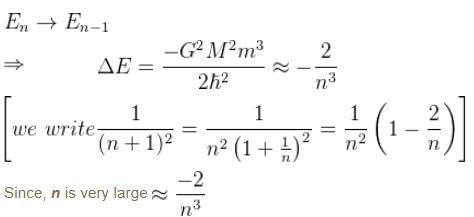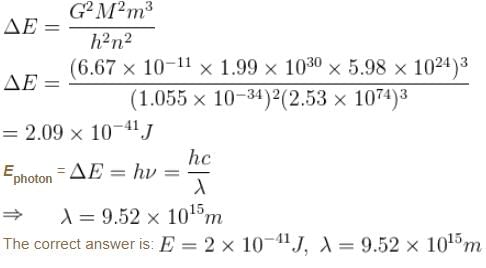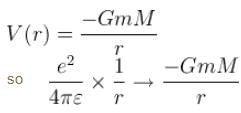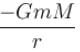Quantum Mechanics In Three Dimensions MCQ - IIT JAM MCQ
10 Questions MCQ Test - Quantum Mechanics In Three Dimensions MCQ
A three dimensional harmonic oscillator is in thermal equilibrium with a temperature reservoir at temperature T. The average total energy of the oscillator is :
Consider the particle in a three dimensional box problem for 2 boxes. One having equal edges of length a and the other of edges 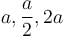 along x, y and z coordinates respectively.
along x, y and z coordinates respectively.
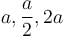 along x, y and z coordinates respectively.
along x, y and z coordinates respectively.What will be quantum number ‘n’ for earth? Take the earth sun distance to be 1.496 × 1011m
Which of the following is true about a quantum harmonic oscillator?
(1) A spectrum of evenly spaced energy states
(2) A potential energy function that is linear in the position coordinate
(3) A ground state characterized by zero kinetic energy.
(4) A non zero probability of finding the oscillator outside the classical turning points.
Which of the following functions could represent the radial wave function for an electron in an atom? (r is the distance of the electron from the nucleus; A, b are constants)
I. Ae–br
II. A sinbr
III. A/r
Suppose the earth made a transition to the next lower level (n – 1). How much energy (in Joules) would be released? What would be the wavelength of the emitted photon be?
Box I has each edge of length ‘a’ units. Box II has edges as a, 2a, a/2 along the x, y and z axis respectively. For what values of nx, ny, nz will the first excited state energy of box II be same as the first excited state energy of Box I
The Energy of the particle is proportional to __________
Consider the Earth-Sun system as a gravitational analog to the hydrogen atom.
What is the potential energy function. (Let m be the mass of earth and M be the mass of the sun)