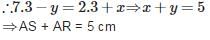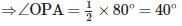RD Sharma Test: Circles - Class 10 MCQ
25 Questions MCQ Test - RD Sharma Test: Circles
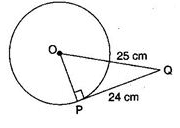
The length of tangent PQ, from an external point P is 24 cm. If the distance of the point P from the centre is 25 cm, then the diameter of the circle is
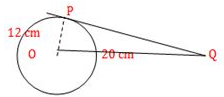
A tangent PQ at point of contact P to a circle of radius 12 cm meets the line through centre O to a point Q such that OQ = 20 cm, length of tangent PQ is :
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such ∠POR = 120∘, then ∠OPQ is
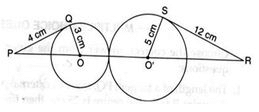
A circle is inscribed in ΔABC having sides 8 cm, 10 cm and 12 cm as shown in the figure. Then,
In the given figure, If TP and TQ are two tangents to a circle with centre O, so that ∠POQ = 110o then ∠PTQ is equal to :
A tangent PQ at a point P o a circle of radius 5 cm meets a line through the centre O at point Q, so that OQ = 12 cm. find the length PQ.
From a point Q, the length of tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm, radius of circle is :
If PA and PB are tangents to the circle with centre O such that ∠APB = 40∘, then ∠OAB is equal to
Quadrilateral PQRS circumscribes a circle as shown in the figure. The side of the quadrilateral which is equal to PD + QB is
In the given figure, the pair of tangents A to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm, then the radius of the circle is :
In the given figure, RQ is a tangent to the circle with centre O. If SQ = 6 cm and RQ = 4 cm, then OR is equal to
In figure, AB is a chord of a circle and AT is a tangent at A such that ∠BAT = 60o, measure of ∠ACB is :
If two tangents inclined at 60∘ are drawn to circle of radius 3 cm, then length of each tangent is equal to
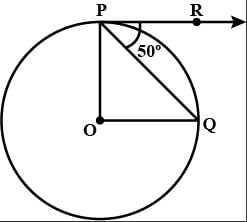
In the given fig., if O is the centre of a circle, PQ is a chord and the tangent PR at P makes an angle of 50∘ with PQ, then ∠POQ is equal to :
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80o, ∠POA is
If PQR is a tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 60∘, then ∠AQB is equal to
In the given figure, a circle touches all four sides of a quadrilateral PQRS, whose sides are PQ = 6.5 cm, QR = 7.3 cm, and PS = 4.2 cm, then RS is equal to
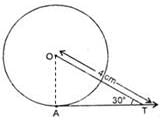
In the given figure, AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30o. Then AT is equal to :
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q, such that OQ = 15 cm. Length of PQ is
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80∘, then find ∠POA.
At one end of a diameter PQ of a circle of radius 5 cm, tangent XPYis drawn to the circle. The length of chord AB parallel to XY and at a distance of 8 cm from P is


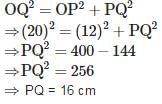

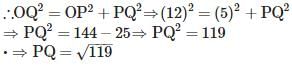
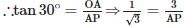
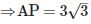 cm Since each tangent from an external point to a circle are equal. Therefore, PA = PB = 3√3 cm
cm Since each tangent from an external point to a circle are equal. Therefore, PA = PB = 3√3 cm