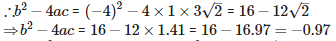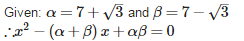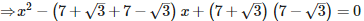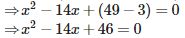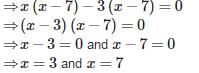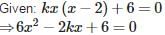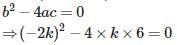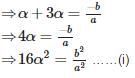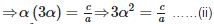RD Sharma Test: Quadratic Equations - Grade 9 MCQ
25 Questions MCQ Test - RD Sharma Test: Quadratic Equations
The common root of 2x2+x−6 = 0 and x2−3x−10 = 0 is
In a cricket matchKumble took three wickets less than twice the number of wickets taken by Srinath. The product of the number of wickets taken by these two is 20, then the number of wickets taken by Kumble is
If the sum and product of the roots of the equation kx2+6x+4k = 0 are equal, then k =
One of the roots of the quadratic equation a2x2−3abx+2b2 = 0 is
The product of two successive integral multiples of 5 is 1050. Then the numbers are
The angry Arjun carried some arrows for fighting with Bheeshma. With half the arrows, he cut down the arrows thrown by Bheeshma on him and with six other arrows he killed the rath driver of Bheeshma. With one arrow each he knocked down respectively the rath, flag and bow of Bheeshma. Finally with one more than four times the square root of arrows he laid Bheeshma unconscious on an arrow bed. The total number of arrows that Arjun had is
If ‘sin α’ and ‘cos α’ are the roots of the equation ax2+bx+c = 0 a then b2 =
The quadratic equation whose roots are 7+√3 and 7−√3 is
The roots of the quadratic equation 9a2b2x2−16abcdx−25c2d2 = 0 are
The constant that must be added and subtracted to solve the quadratic equation by the method of completing the square is
Which of the following has two distinct roots?
If ‘a’ and ‘b’ are the roots of the equation x2+ax+b = 0, then a+b =
If x = 2 is a root of the quadratic equation 3x2 – px – 2 = 0, then the value of ‘p’ is
The sum of reciprocals of Sharma’s age 3 years ago and 5 years from now is 1/3, then his present age is
If ax2+bx+c = 0 has equal roots, then c is equal to
If the quadratic equation kx(x – 2) + 6 = 0 has equal roots, then the value of ‘k’ is
If one root of the equation ax2+bx+c = 0 is three times the other, then b2 : ac =
A train travels 360km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey, then the actual speed of the train is
Let b = a + c. Then the equation ax2+bx+c = 0 has equal roots if
The discriminant of the quadratic equation 3√3x2+10x+√3 = 0 is
If one root of the equation 4x2−2x+(λ−4) = 0 be the reciprocal of the other, then the value of is