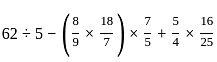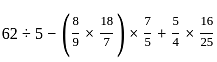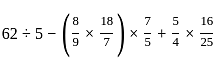RRB NTPC CBT 1 Question Paper (Held On: 29 Dec 2020 Shift 1) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test RRB NTPC - Previous Year Papers (Hindi) - RRB NTPC CBT 1 Question Paper (Held On: 29 Dec 2020 Shift 1)
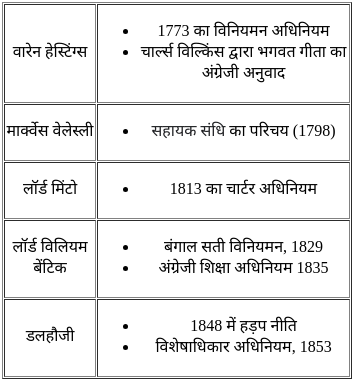
निम्नलिखित में से कौन-सा बाघ अभयारण्य है?
हल कीजिए:
cos 20° cos 40° cos 80°
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
चिश्ती सिलसिला के सबसे महत्वपूर्ण शिक्षकों में से एक, शेख मोइनुद्दीन चिश्ती दरगाह _______ में स्थित है।
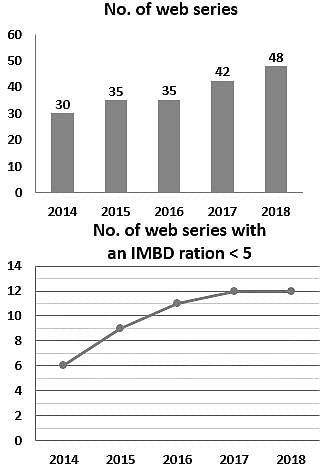
निम्नलिखित दंड आलेख 2014-2018 तक विभिन्न वर्षो में एक सदस्यता सेवा मोबाइल एप्लिकेशन द्वारा जारी की गयी वेब सीरीजों की संख्या को दर्शाती है और रेखा आलेख 5 स्टार से कम रेटिंग वाले वेब सीरीजों की संख्या को दर्शाती है। तो 2014 से 2018 तक 5 स्टार और उससे अधिक रेटिंग वाले वेब सीरीज का अनुमानित कुल प्रतिशत ज्ञात कीजिए।
100 से 200 के बीच ऐसी सभी संख्याओं का योग ज्ञात कीजिए जो 12 से विभाज्य हैं?
सरल कीजिए:
24 + 7.2 ÷ 8 - 3 × 2.3 + 5
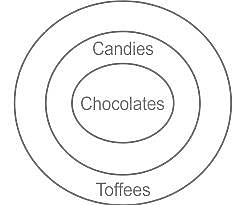
दिए गए कथनों और निष्कर्षों को ध्यानपूर्वक पढ़िए। यह मानते हुए कि कथनों में दी गई जानकारी सत्य है, भले ही वह सामान्यतः ज्ञात तथ्यों से भिन्न प्रतीत होती हो, तय कीजिये कि दिए गए निष्कर्षों में से कौन-सा/से निष्कर्ष कथनों का तार्किक रूप से अनुसरण करता/करते है/हैं।
कथन:
1. सभी चॉकलेट कैंडी हैं।
2. सभी कैंडी टॉफी हैं।
निष्कर्ष:
1. सभी चॉकलेट टॉफी हैं।
2. सभी टॉफी चॉकलेट हैं।
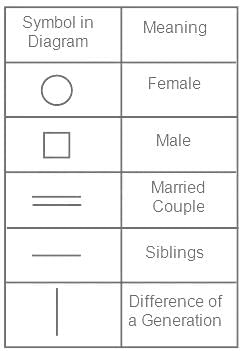
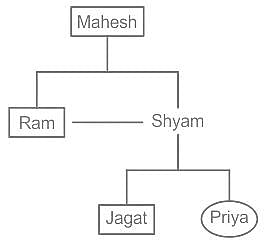
राम, श्याम का भाई है और महेश, राम का पिता है। जगत, प्रिया का भाई है और प्रिया, श्याम की पुत्री है। महेश, जगत से किस प्रकार संबंधित है?
उस विकल्प का चयन कीजिए, जो तीसरे पद से उसी प्रकार संबंधित है जिस प्रकार दूसरा पद, पहले पद से संबंधित है।
बिल्ली : फेलाइन :: कुत्ता : ?
यदि 2x + 5y = 12, xy = 2, तो 8x3 + 125y3 का मान ज्ञात कीजिए।
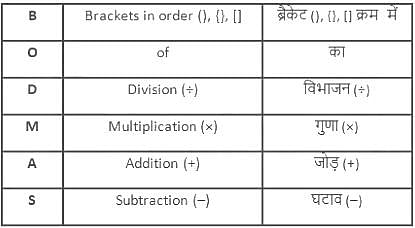
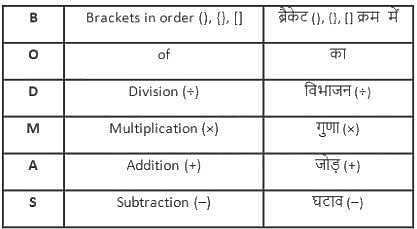
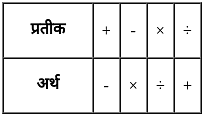
यदि 'p + q' का अर्थ 'p - q', 'p - q' का अर्थ 'p × q', 'p × q' का अर्थ 'p ÷ q' और 'p ÷ q' का अर्थ 'p + q' है, तो 25 + 48 × 6 ÷ 12 - 2 का मान ज्ञात कीजिए।
दिए गए विकल्पों में से उस संख्या का चयन कीजिए जो निम्नलिखित शृंखला में प्रश्न चिन्ह (?) को प्रतिस्थापित कर सकती है।
3, 16, 125, ?
आपको तर्कों के 3 समूह दिए गए हैं, जिनमें से प्रत्येक में तीन कथन हैं। उस समूह का चयन कीजिए जिसमें तीसरा कथन पहले दो कथनों का तार्किक निष्कर्ष है।
A. (i) सभी दुकानें शोरूम हैं।
(ii) कोई शोरूम मॉल नहीं है।
(iii) सभी दुकानें मॉल नहीं हैं।
B (i) कोई भी जापानी नृत्य नहीं कर सकता है।
(ii) सभी अमेरिकी किताबें हैं।
(iii) अमेरिकी और जापानी नृत्य कर सकते हैं।
C. (i) कोई P, Q नहीं है।
(ii) कोई Q, R नहीं है।
(iii) कोई P, R नहीं है।
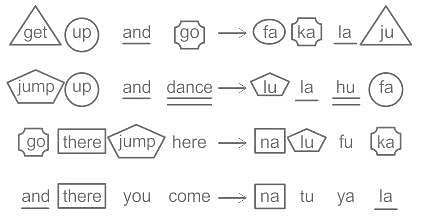
एक निश्चित कूट भाषा में, 'get up and go' को 'fa ka la ju' लिखा जाता है, 'jump up and dance' को 'lu la hu fa' लिखा जाता है, 'go there jump here' को 'na lu fu ka' लिखा जाता है और 'and there you come' को 'na tu ya la' लिखा जाता है। उस भाषा में 'get up go there' को किस प्रकार लिखा जाएगा?
|
33 docs|20 tests
|
|
33 docs|20 tests
|