RRB NTPC CBT 2 (Level-3) Question Paper (Held On: 14 June 2022 Shift 1) - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test RRB NTPC - Previous Year Papers (Hindi) - RRB NTPC CBT 2 (Level-3) Question Paper (Held On: 14 June 2022 Shift 1)
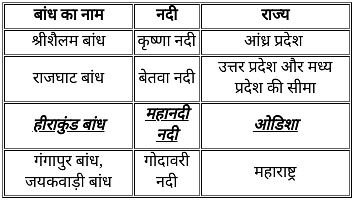
हीराकुंड बांध जो कि दुनिया के सबसे बड़े बांधों में से एक है, ______ नदी पर बनाया गया है।
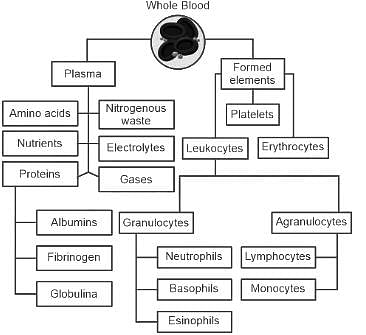
मानव रक्त का तरल भाग, जिसे ________ कहा जाता है, जल, लवण और प्रोटीन से बना होता है।
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
दिसंबर 2021 में भारतीय सेना ने किसके सहयोग से मध्य प्रदेश में क्वांटम लैब की स्थापना की?
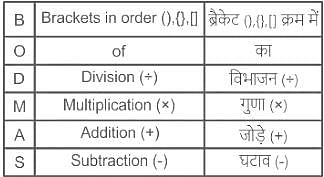
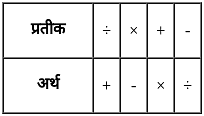
यदि '÷' को '+' से प्रतिस्थापित किया जाता है,'×' को '-' से प्रतिस्थापित किया जाता है,'+' को '×' से प्रतिस्थापित किया जाता है और '-' को '÷' से प्रतिस्थापित किया जाता है, तो दिए गए व्यंजक का मान क्या होगा?
8 + 5 × 54 - 9 ÷ 3 = ?
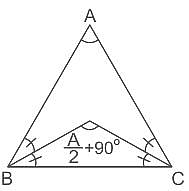
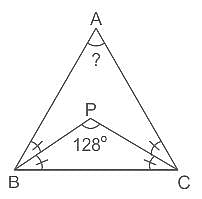
ΔABC में, ∠B और ∠C के समद्विभाजक त्रिभुज के अंदर P पर प्रतिच्छेद करते हैं। यदि ∠BPC = 128° है, तो ∠A की माप क्या है?
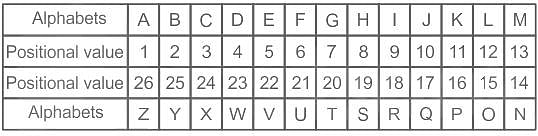
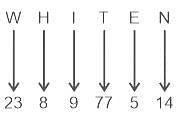
एक निश्चित कूट भाषा में, अंग्रेजी वर्णमाला के अक्षरों को उनके वर्णमाला क्रम (A को 1 और Z को 26) के अनुसार कूटबद्ध किया जाता है। हालांकि, यदि किसी व्यंजन के ठीक बाद और ठीक पहले एक स्वर हो, तो उसका कूट '77' होगा।
इस भाषा में 'WHITEN' के लिए क्या कूट होगा?
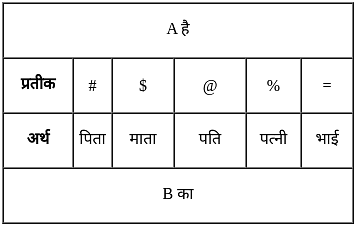
यदि
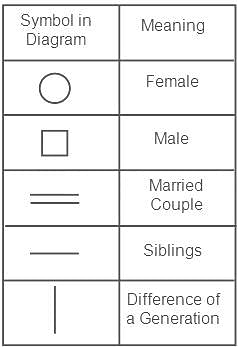
'A # B' का अर्थ है कि 'A, B का पिता है',
'A $ B' का अर्थ है कि 'A, B की माता है',
'A @ B' का अर्थ है कि 'A, B का पति है',
'A % B' का अर्थ है कि 'A, B की पत्नी है'
'A = B' का अर्थ है कि 'A, B का भाई है',
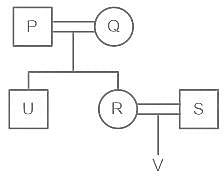
तो निम्नलिखित व्यंजक में P, V से किस प्रकार संबंधित है?
P @ Q $ U = R % S # V
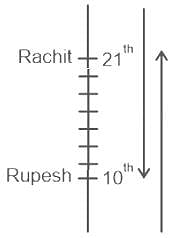
मध्यावधि परीक्षा के बाद रूपेश शीर्ष से 10वें और रचित नीचे से 21वें स्थान पर थे। यदि रचित ने रूपेश से बेहतर प्रदर्शन किया और उनके बीच छह विद्यार्थियों के स्थान हैं, तो कितने विद्यार्थी परीक्षा में उपस्थित हुए?
त्रिपुरा के सत्यराम रियांग, जिन्हें 2021 में पद्म श्री पुरस्कार मिला, एक प्रसिद्ध _______ नर्तक हैं।
एक आयताकार खेत का क्षेत्रफल, जिसकी भुजाएँ 13 : 5 के अनुपात में हैं, 260 मीटर² है। आयताकार खेत का परिमाप क्या है?
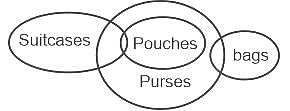
दिए गए कथनों और निष्कर्षों को ध्यानपूर्वक पढ़िए। यह मानते हुए कि कथनों में दी गई जानकारी सत्य है, भले ही वह सामान्य रूप से ज्ञात तथ्यों से भिन्न प्रतीत होती हो, तय कीजिये कि दिए गए निष्कर्षों में से कौन-सा कथनों का तार्किक रूप से अनुसरण करता है।
कथन:
a) कुछ सूटकेस पाउच हैं।
b) कुछ बैग पर्स हैं।
c) सभी पाउच पर्स हैं।
निष्कर्ष:
I. कुछ सूटकेस पर्स हैं।
II. कुछ पर्स बैग हैं।
III. सभी पर्स पाउच हैं।
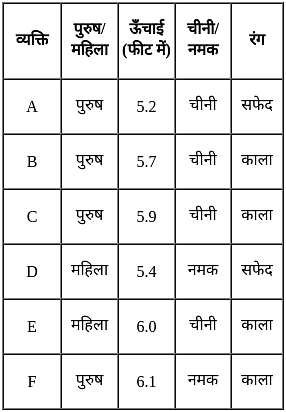
छह लोग, A, B, C, D, E और F हैं। A, B, C और F पुरुष हैं और अन्य दो महिलाएं हैं। A की लंबाई 5.2 फीट है, B की लंबाई 5.7 फीट है, C की लंबाई 5.9 फीट है, D की लंबाई 5.4 फीट है, E की लंबाई 6.0 फीट है और F की लंबाई 6.1 फीट है। इन सभी में से A, B, C और E को चीनी पसंद है तथा D और F को नमक पसंद है। जिन लोगों की लंबाई 5.5 फीट से अधिक है वे काले रंग के और अन्य सफेद रंग के कपड़े पहनते हैं।
इनमें से कौन चीनी पसंद करने वाला पुरुष है जो काले रंग का कपड़ा नहीं पहनता है?
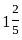 वर्ष के लिए 10% प्रति वर्ष की दर से निवेश की गई ₹19,500 की राशि पर चक्रवृद्धि ब्याज क्या होगी यदि चक्रवृद्धि ब्याज वार्षिक रूप से संयोजित होता है?
वर्ष के लिए 10% प्रति वर्ष की दर से निवेश की गई ₹19,500 की राशि पर चक्रवृद्धि ब्याज क्या होगी यदि चक्रवृद्धि ब्याज वार्षिक रूप से संयोजित होता है?
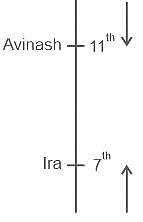
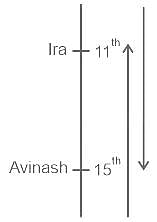
अविनाश कक्षा में शीर्ष से 11वें स्थान पर और इरा नीचे से 7वें स्थान पर है। यदि उनके स्थान परस्पर बदल जाते हैं, तब अविनाश शीर्ष से 15वें स्थान पर होगा और इरा नीचे से 11वें स्थान पर होगी। परीक्षा के लिए कुल कितने विद्यार्थी उपस्थित हुए थे?
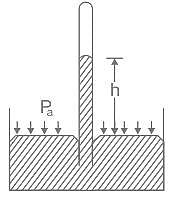
वायुमंडलीय दाब को मापने के लिए निम्नलिखित में से किस उपकरण का उपयोग किया जाता है?
|
33 docs|20 tests
|
|
33 docs|20 tests
|


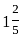 वर्ष
वर्ष