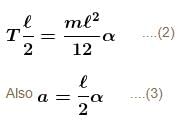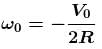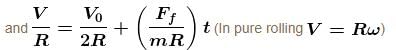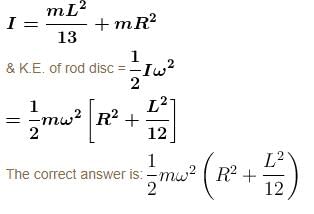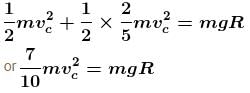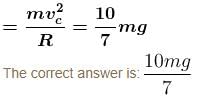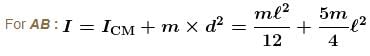Rigid Body Dynamics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Rigid Body Dynamics MCQ Level - 2
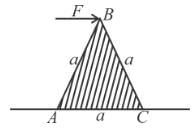
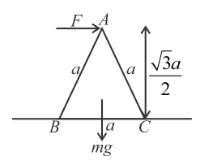
A uniform equilateral prism of mass m rests on a rough horizontal surface with coefficient of friction mu. A horizontal force F is applied on the prism as shown in the figure. If the coefficient of friction is sufficiently high so that the prism does not slide before topping, then the minimum force required to topple the prism is :

Two points of a rod move with velocities 3v and v perpendicular to the rod and in the same direction, separated by a distance r. Then the angular velocity of the rod is :
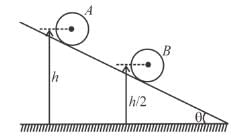
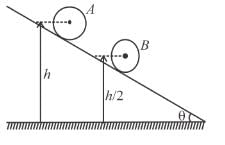
Two identical uniform solid spherical balls A and B of mass m each are placed on a fixed wedge as shown in figure. Ball B is kept at rest and it is released just before two balls collides. Ball A rolls down without slipping on inclined plane and collide elastically with ball B. The kinetic energy of ball A just after the collision with ball B is :

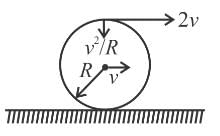
A uniform ring of radius R rolls without sliding. The radius of curvature of the path followed by any particle of the ring at the highest point of its path will be :
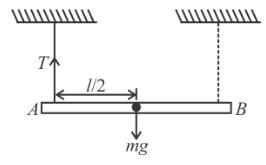
A uniform thin rod of mass m and length L is held horizontally by two vertical strings attached to the two ends. One of the string is cut. Find the angular acceleration soon after it is cut :
A uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be :
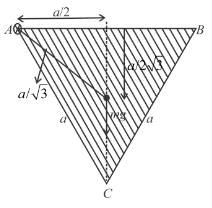
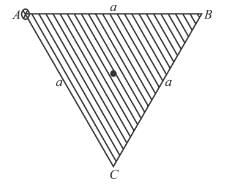
A uniform triangular plate ABC of mass m and moment of inertia I (about an axis passing  through A and perpendicular to plane of the plate) can rotate freely in the vertical plane about point A as shown in figure. The plate is released from the position shown in the figure. Line AB is horizontal. The acceleration of centre of mass just after the release of plate is :
through A and perpendicular to plane of the plate) can rotate freely in the vertical plane about point A as shown in figure. The plate is released from the position shown in the figure. Line AB is horizontal. The acceleration of centre of mass just after the release of plate is :
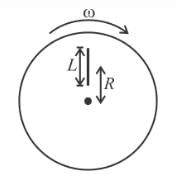
A uniform rod of mass M and length L lies radially on a disc rotating with angular speed ω in a horizontal plane about its axis. The rod does not slip on the disc and the centre of the rod is at a distance R from the centre of the disc. Then the kinetic energy of the rod is :
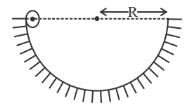
In the figure shown, a small solid spherical ball of mass m can move without sliding in a fixed semicircular track of radius R in vertical plane. It is released from the top. The resultant force on the ball at the lowest point of the track is :
A uniform thin rod of length 4l, mass m is bent at the points as shown in the figure. What is the moment of inertia of the rod about the axis passing through point O and perpendicular to the plane of the paper.




 vrel bring the velocity of one point w.r.t. other
vrel bring the velocity of one point w.r.t. other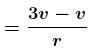 and r being the distance between them
and r being the distance between them
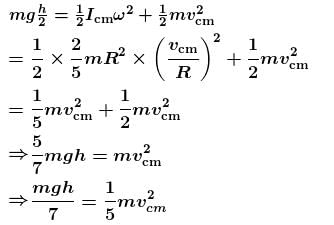
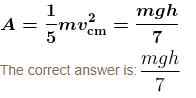
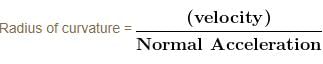
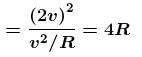
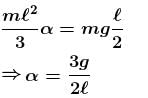
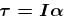 about centre of mass
about centre of mass