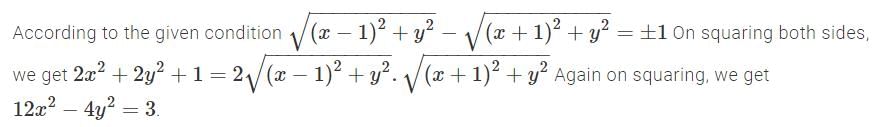EduRev

Courses

Get the App Signup / Login

Welcome Back

Forgot Password?

New User? Sign Up

Create your account now

I accept the Terms & Conditions.

Already Have an Account? Login

SRMJEEE Maths Mock Test - 2

35 Questions MCQ Test SRMJEEE Subject Wise & Full Length Mock Tests | SRMJEEE Maths Mock Test - 2

Description

Attempt SRMJEEE Maths Mock Test - 2 | 35 questions in 50 minutes | Mock test for JEE preparation | Free important questions MCQ to study SRMJEEE Subject Wise & Full Length Mock Tests for JEE Exam | Download free PDF with solutions

QUESTION: 1

Every continuous function is

A.
increasing
B.
decreasing
C.
not differentiable always
D.
differentiable

Solution:

QUESTION: 2

Area bounded by the curve xy² = a² (a - x) and y-axis is

A.
π a²/2
B.
π a²
C.
3 π a²
D.
3 π a²/2

Solution:

QUESTION: 3

Let f(x) = [cos x + sin x], 0 < x < 2π where [x] denotes the greatest integer less than or equal to x. The number of points of discontinuity of f(x) is

A.
6
B.
5
C.
4
D.
3

Solution:

We know that [x] is discontinuous at integral values of x.

QUESTION: 4

Equation of the circle having diameters 2x - 3y = 5 and 3x - 4y = 7 and radius 8 is

A.
x² + y² - 2x + 2y - 62 = 0
B.
x² + y² + 2x + 2y - 2 = 0
C.
x² + y² + 2x - 2y - 62 = 0
D.
none of these

Solution: The intersection of the diagonals i.e. (1,-1) is the centre of the circle with radius 8. put in the formula
(x-1)^2+(y+1)^2=8^2
x2+y2-2x+2y-62=0

QUESTION: 5

Coordinates of two points are A(1,0) and B(-1,0) and Q is a point which satisfies AQ-BQ = + 1. The locus of the point Q is

A.
12x²+4y²=3
B.
12x²-4y²=3
C.
12x²-4y²+3=0
D.
12x²+4y²+3=0

Solution: Option B is correct.

QUESTION: 6

The term independent of x in the expansion of ((2x) - (3/x))⁶ is

A.
4320
B.
216
C.
-216
D.
-4320

Solution:

QUESTION: 7

The equation of tangent at point (1,2) to the parabola y²=4x is

A.
x-y+1=0
B.
x+y+1=0
C.
x+y-1=0
D.
x-y-1=0

Solution:

QUESTION: 8

The number of solutions of the equation

A.
1
B.
2
C.
3
D.
4

Solution:

QUESTION: 9

The area bounded by the curve y=sinx, y=0, x=0 and x=(π/2) is

A.
π
B.
2π
C.
1
D.
2

Solution:

QUESTION: 10

The family of curves, in which the subtangent at any point to any curve is double the abscissa, is given by

A.
x = cy²
B.
y = cx²
C.
x² = cy²
D.
y = cx

Solution:

QUESTION: 11

If the matrix is singular one, then λ is

A.
3
B.
4
C.
2
D.
5

Solution:

QUESTION: 12

∫x sec²x dx=

A.
tan x²
B.
tan²x
C.
x tanx-log sinx
D.
x tanx+log cosx

Solution:

QUESTION: 13

A.
Sin⁻¹ x
B.
C.
D.
e^Sin−1 x

Solution:

QUESTION: 14

A.
1
B.
- 1
C.
- 1/2
D.
1/2

Solution:

QUESTION: 15

A.
51/65
B.
52/65
C.
56/65
D.
None of these

Solution:

QUESTION: 16

If A and B are 2 x 2 matrices then (A+B)²=

A.
A²+2AB+B²
B.
A²+AB+BA+B²
C.
A²+2BA+B²
D.
none of these

Solution:

QUESTION: 17

The ratio of the altitude of the cone of greatest volume which can be inscribed in a given sphere to the diameter of the sphere is

A.
2/3
B.
3/4
C.
1/3
D.
1/4

Solution:

QUESTION: 18

The mean of 3, y, 4, x, 10, is 5, then y =

A.
8 - x
B.
5 - x
C.
Smaller than x but not related to n
D.
None of the above

Solution:

QUESTION: 19

The inverse of matrix

A.
B.
C.
D.
None of these

Solution:

QUESTION: 20

In a certain distribution, the following results were obtained , Median = 48, Coefficient of skewness = -0.3.

What is the value of standard deviation?

A.
20
B.
25
C.
28
D.
30

Solution:

QUESTION: 21

The angle between lines y²sin²θ-xysin²θ+x²(cos²θ-1) = 1 is

A.
π/3
B.
π/4
C.
2π/3
D.
π/2

Solution:

QUESTION: 22

Three identical dice are rolled. The probability that the same number will appear on each of them is

A.
1/36
B.
1/18
C.
1/6
D.
3/18

Solution:

QUESTION: 23

If the sides of a triangle are proportional to the cosines of the opposite angles then the triangle is

A.
right angled
B.
equilateral
C.
obtuse angled
D.
none of these

Solution:

QUESTION: 24

If the difference between the corresponding roots of x² + ax + b = 0 and x² + bx + a = 0 is same and a ≠ b, then

A.
a + b + 4 = 0
B.
a + b - 4 = 0
C.
a - b - 4 = 0
D.
a - b + 4 = 0

Solution:

QUESTION: 25

If A.M. between two numbers is 5 and their G.M. is 4, then their H.M. is

A.
16/5
B.
14/5
C.
11/5
D.
none of these

Solution:

If x, y and z respectively represent AM, GM and HM between two numbers a and b, then
y² = xz
Here x = 5, y = 4
then 16 = 5 x z
z = 16/5

QUESTION: 26

The number of 4-digit even numbers that can be formed using 0, 1, 2, 3, 4, 5, 6 without repetition is

A.
120
B.
300
C.
420
D.
20

Solution:

Each even number must have 0, 2, 4 or 6 in is units place
Here total number of digits = 7

When 0 occurs at units place there is no restriction on other places and when 2 or 4 occurs at units place there is restriction on thousands' place as 0 can not be put at thousands' place
Case I When 0 occurs at units place:

∴ The number of numbers formed in this case

Case II. When 0 does not occur at units place:

The units' place can be filled up by any one of the three digits 2, 4 and 6 in 3 ways
∴ The number of numbers formed in this case

∴ The required number = 120 + 300 = 420

QUESTION: 27

A condition for a function y = f (x) to have an inverse is that it should be

A.
defined for all x
B.
continuous every where
C.
an even function
D.
strictly monotone and continuous in the domain

Solution:

QUESTION: 28

The derivative of is given by

Solution:

QUESTION: 29

A line passing through point A(-5,-4) meet other three lines x + 3y + 2 = 0, 2x + y + 4 = 0 and x - y - 5 = 0 at B, C and D respectively. If (15/AB )² + (10/AC)² = (6/AD)², then the equation of line is

A.
2x+3y+22=0
B.
5x-4y+7=0
C.
3x-2y+3=0
D.
3x+2y+3=0

Solution:

Equation of any line through A(-5, -4) is

then the coordinates of any point on this line at a distance r from A are
(r cosθ - 5, r sinθ - 4)
If AB = r₁, AC = r₂, AD = r₃
then (r₁ cosθ - 5, r₁ sinθ - 4) lies on x + 3y + 2 = 0
⇒ r₁ cosθ - 5 + 3 (r₁ sinθ - 4) + 2 = 0
⇒ r₁ (cosθ + 3 sinθ) = 15

Therefore according to the given condition

Hence the required equation of the line is