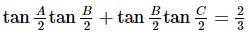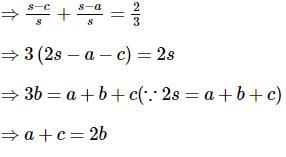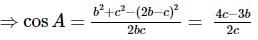SRMJEEE Maths Mock Test - 5 - JEE MCQ
30 Questions MCQ Test - SRMJEEE Maths Mock Test - 5
The number of real values of k for which the lines 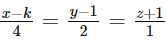 and
and 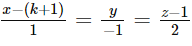 are intersecting is
are intersecting is
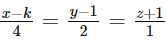 and
and 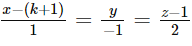 are intersecting is
are intersecting isConsider the given expression:
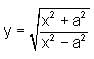
Differentiate y with respect to x.
A canonical plastic bottle whose height is 21 m and radius of base is 7 m is being filled with milk at a uniform rate of 5/3 m3/min. When the milk level is 6 m, find the rate at which the level of the milk in the bottle is rising.
The number of surjections from A = {1,2, ...n), n > 2 onto B = (a,b) is
A circle inscribed in a triangle ABC touches the side AB at D such that AD=5 and BD=3 . If ∠A=60°, then the value of [BC/3] (where [.] represents greatest integer function) is
Consider the following expression:
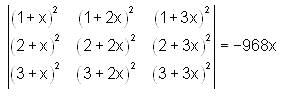
The number of values of x which satisfy the given expression is
If P and Q are two sets such that 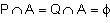 and
and 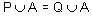 for same set A, then which of the following options is correct?
for same set A, then which of the following options is correct?
If A is the area and 2s the sum of three sides of a triangle, then
Find the area (unit2) bounded by the two curves y = 6 + 5x - 2x2 y = 2x + 3.
If a1 a2, a3 are in G.P. with common ratio r, then value of a3 > 4a2 - 3a1 holds if
The number of ways in which one or more balls can be selected out of 10 white, 9 green and 7 blues balls, is
If 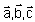 are three non-coplanar vectors and
are three non-coplanar vectors and 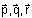 are vectors defined by the relations
are vectors defined by the relations 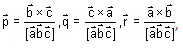 then the value of
then the value of 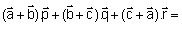
The number of bijective functions from set A to itself when A contains 106 elements is
If a∈ z, ( x - a ) (x - 10) + 1 = 0 has integral roots, then values of a are
If 4 cos A cos B + sin 2A + sin 2B +sin 2C = 4 , then ΔABC is
The equation of a circle C1 is x2 + y2 − 4x − 2y − 11 = 0. Another circle C2 of radius 1 unit rolls on the outer surface of the circle C1. Then the equation of the locus of the centre of C2 is
The axis of a parabola is along the abscissa. Its vertex is at origin and it passes through a point P(2, 3). The equation of the parabola is
In a ΔABC, (b+c)cosA+(c+a)cos B+(a+b) cosC equals to ( where a,b and c are the lengths of the side opposite to angles A,B and C respectively )
The mean of n items is 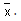 If these n items are successively increased by 2, 22, 23, …, 2n, then the new mean is
If these n items are successively increased by 2, 22, 23, …, 2n, then the new mean is
The locus of point z satisfying Re 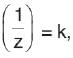 when k is a non-real real number is
when k is a non-real real number is
In a ΔABC , if a=4 cm, b=6 cm and c=8 cm , then r equals
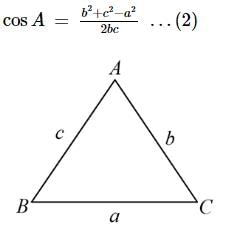
If the sides of a Δ ABC are in A.P. and a is the smallest side, then cosA equals:



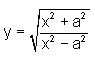
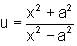
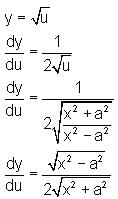
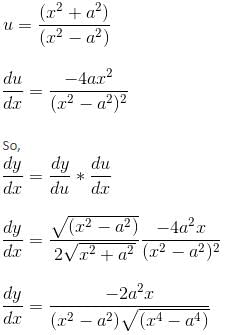
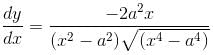
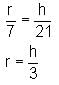
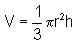
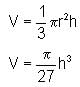
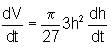
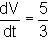
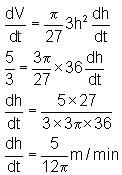
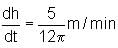

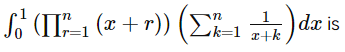
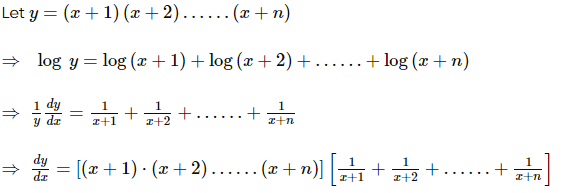
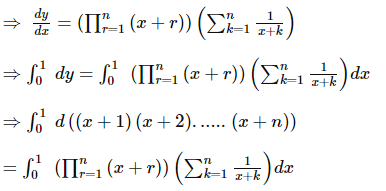
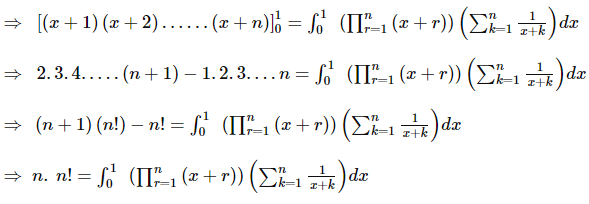
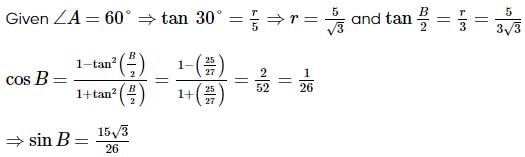
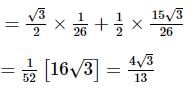
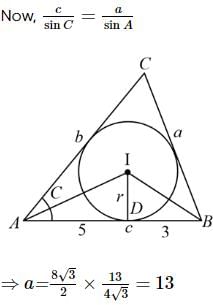

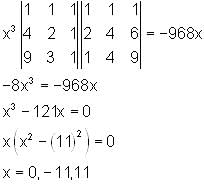
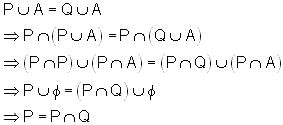
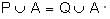
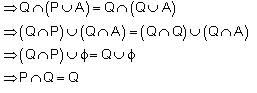

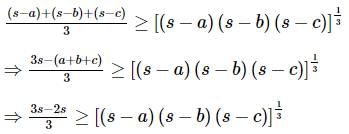
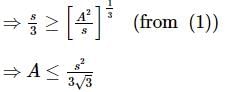


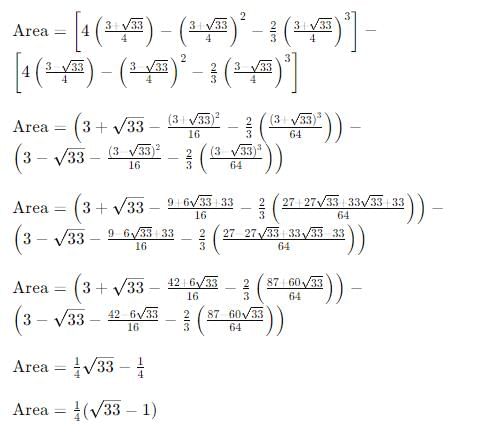
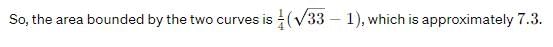
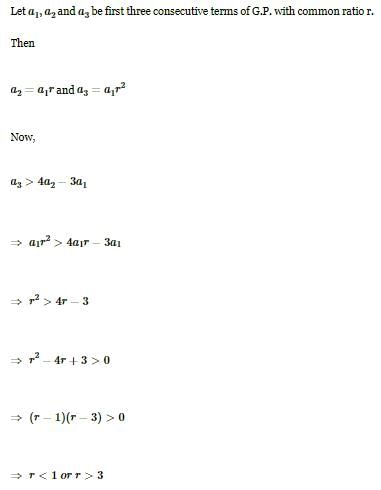
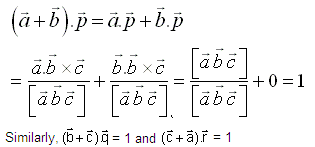
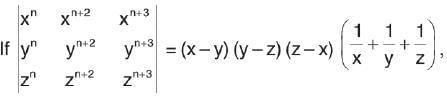
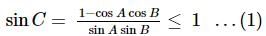
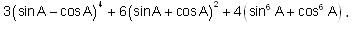
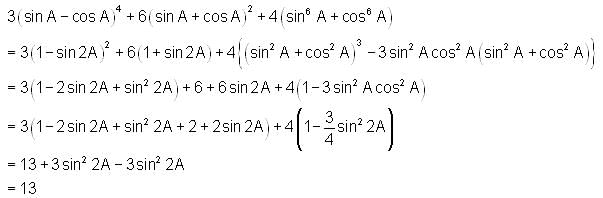
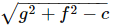
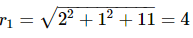
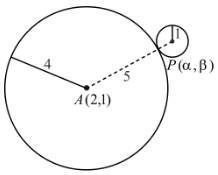
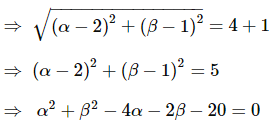
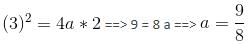
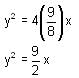
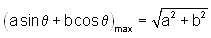
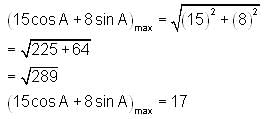
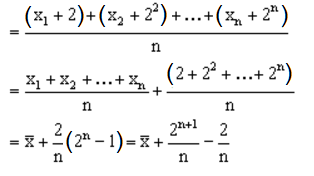


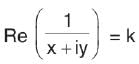
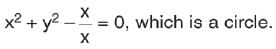
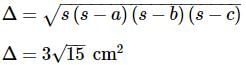
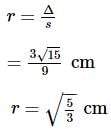
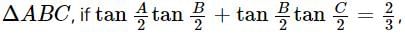 then a+c is equal to
then a+c is equal to