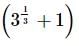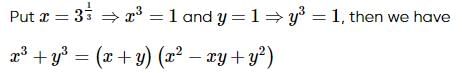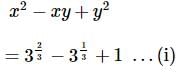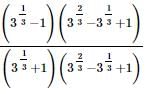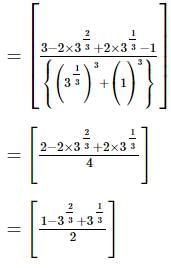SRMJEEE Maths Mock Test - 8 - JEE MCQ
30 Questions MCQ Test - SRMJEEE Maths Mock Test - 8
If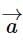 and
and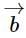 are two unit vectors such that
are two unit vectors such that are perpendicular to each other, then the angle between
are perpendicular to each other, then the angle between 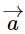 and
and 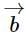 is
is
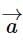 and
and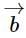 are two unit vectors such that
are two unit vectors such that are perpendicular to each other, then the angle between
are perpendicular to each other, then the angle between 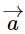 and
and 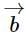 is
isLet the unit vectors 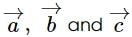 be the position vectors of the vertices of ΔABC. If
be the position vectors of the vertices of ΔABC. If 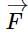 is the position vector of the mid-point of the line segment joining its orthocentre and centroid, then
is the position vector of the mid-point of the line segment joining its orthocentre and centroid, then 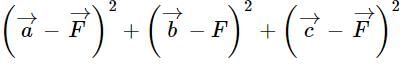 is equal to
is equal to
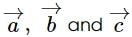 be the position vectors of the vertices of ΔABC. If
be the position vectors of the vertices of ΔABC. If  is the position vector of the mid-point of the line segment joining its orthocentre and centroid, then
is the position vector of the mid-point of the line segment joining its orthocentre and centroid, then 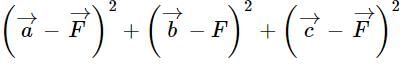 is equal to
is equal toConsider the function given below:

Which of the following statements is true?

Which of the following statements is true?
Points of intersection of a plane on the coordinate axes are P, Q and R. If (a, b, c) is the intersection point of the medians of ∆PQR, then what is the equation of the plane?
A person is to select an onto function from all the functions F: A → A, where A = {2, 4, 6, 8, 10, 12, 14}. Find the probability of selecting onto function.
If 1 + sin x + sin 2 x + … ∞ = 4 + 2 √ 3 , 0 < x < π , x ≠ π/2 then x =
The differential coefficient of log (I log xl) with respect to log x is
The total number of solutions of the system of equations 5x−y=3,y2−6x2=25 are
Let A(1,−1,2) A and B(2,3,−1) be two points. If a point P P divides AB AB internally in the ratio 2:3, then the position vector of P is
Length of the tangent from (2,1) to the circle x2 + y2 + 4y + 3 = 0 is
The number of roots of the equation 2sin2θ + 3sinθ + 1 = 0 in 0,2π is
Let P(x) = x2 + xQ'(1) + Q'(2) and Q(x) = x2 + xP'(2) + P'(3), then
Consider the equations given below:
y = (1 - x)2
y = 0
x = 0
A straight line representing x = k separates the area enclosed by the above curves. Say both the areas are A1 (0 ≤ x ≤ k) and A2 (k ≤ x ≤ 1). If A1 - A2 = 1/4 , then what is the value of k?
 are n-rowed square matrices such that
are n-rowed square matrices such that 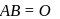 and
and 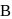 is non-singular. Then
is non-singular. Then
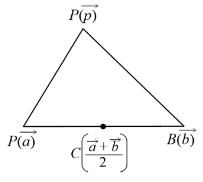
If C is the midpoint of AB and P is any point outside AB, then
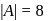 , where
, where 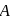 is square matrix of order 3, then what is
is square matrix of order 3, then what is 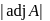 equal to?
equal to?
The area enclosed between the curves y = x2 and x = y2 is


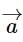 and
and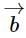
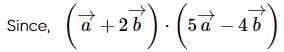
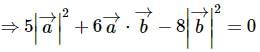
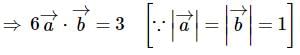
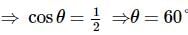
 and the centroid is
and the centroid is 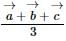
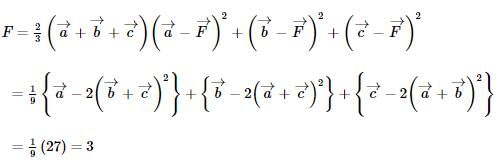

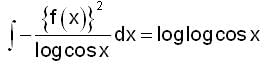
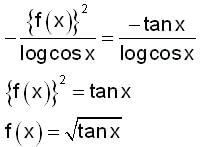
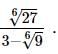
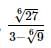
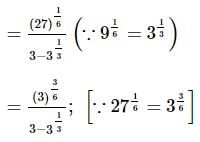
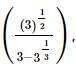 we will first obtain the rationalising factor of
we will first obtain the rationalising factor of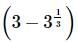
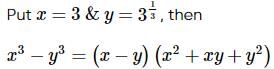
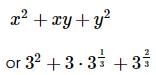
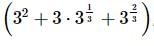 we get
we get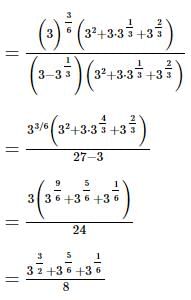
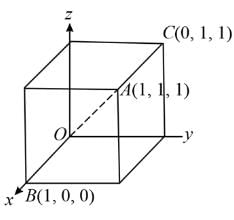
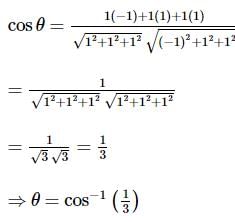
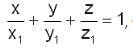 where x1, y1 and z1 are the intercepts made by the plane on the axes.
where x1, y1 and z1 are the intercepts made by the plane on the axes.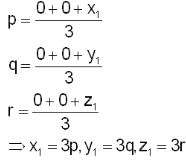
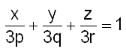


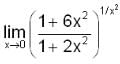
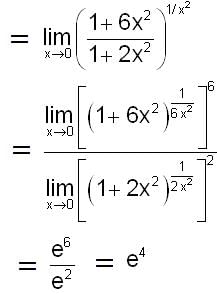
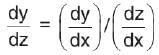
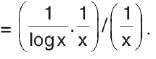
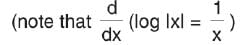
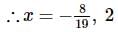
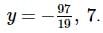
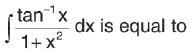
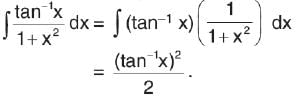
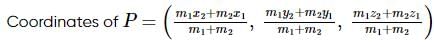
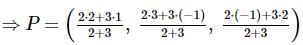
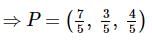
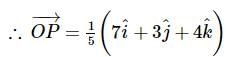
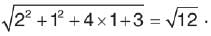
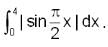
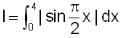
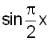 is positive when 0 < x < 2, and negative when 2< x < 4.
is positive when 0 < x < 2, and negative when 2< x < 4.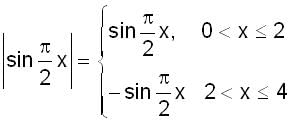
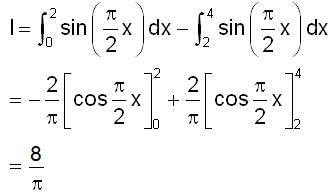
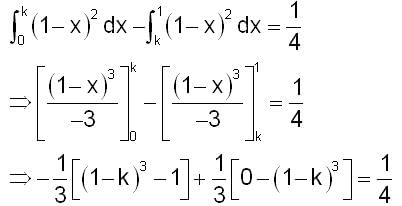
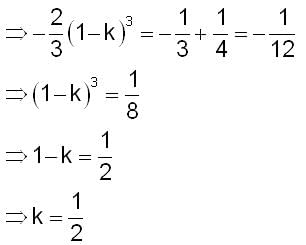
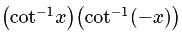 is
is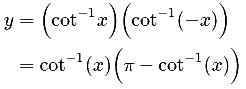
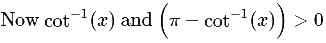
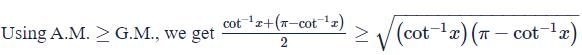
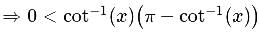
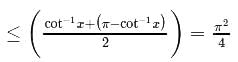
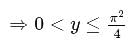
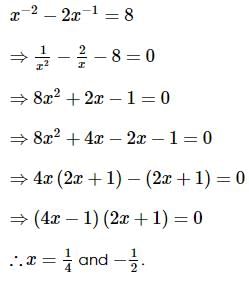
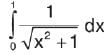 is equal to
is equal to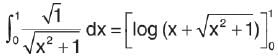
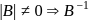 exists,
exists, 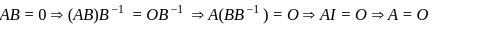
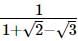 is equivalent to
is equivalent to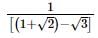
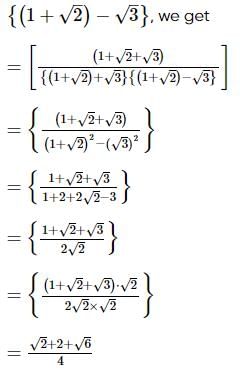
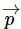

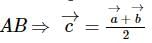
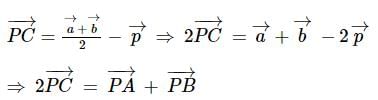
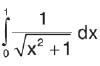 is equal to
is equal to 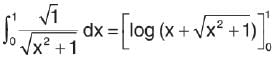
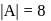 and
and 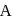 is a square matrix of order 3 . We know that
is a square matrix of order 3 . We know that  I where
I where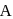 .
.
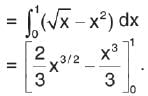
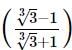 with rational denominator.
with rational denominator.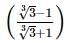
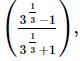 we will first obtain the rationalising factor of
we will first obtain the rationalising factor of