Sample BITSAT Maths Test - JEE MCQ
30 Questions MCQ Test - Sample BITSAT Maths Test
What is the area under the curve y = |x| + | x - 1| between x = 0 and x = 1 ?
The greatest term in the expansion of (3 + 2x)9, when x = 1, is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The coordinates of the pole of the line lx+my+n=0 with respect to the circle x2+y2=1 are
If the line 2x - y + k = 0 is a diameter of the circle x2 + y2 + 6x -6y + 5 =0, then k is equal to
The differential equation of the family of lines passing through the origin is
Which of the following is a solution of the differential equation 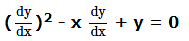
Value of 1 + log x + (log x)2/2! + (log x)3/3! + ..... ∞ is
The angle of elevation of a cloud from a point h mt above the surface of a lake is θ and the angle of depression of its reflection in the lake is φ . The height of the cloud is
The eccentricity of the conjugate hyperbola of the hyperbola x2 - 3y2 = 1 is
Which of the following functions is a solution of the differential equation (dy/dx)2 - x (dy/dx) + y = 0?
The solution of the differential equation (dy/dx) = (y/x) + (φ (y/x)/φ' (y/x)) is
If A, B are two square matrices such that AB = A and BA = B, then
For a square matrix A, it is given that AA' = I, then A is a
The real value of α for which the expression 1-i sin α/1+2 i sin α is purely real is
The equation of the normal to the curve x2 = 4y at (1, 2) is
Two finite sets have m and n elements, the total number of subsets of the first set is 56 more than the total number of subsets of the second. The value of m and n are respectively
In how many ways can the letters of the word ARRANGE be arranged so that R's are never together?
A and B are events such that P(A ∪ B) = 3/4, P(A ∩ B) = 1/4, P(A̅)= 2/3, then P(A̅ ∩ B) is
The probability that a number selected at random from the set of numbers {1,2,3,....,100} is a cube is


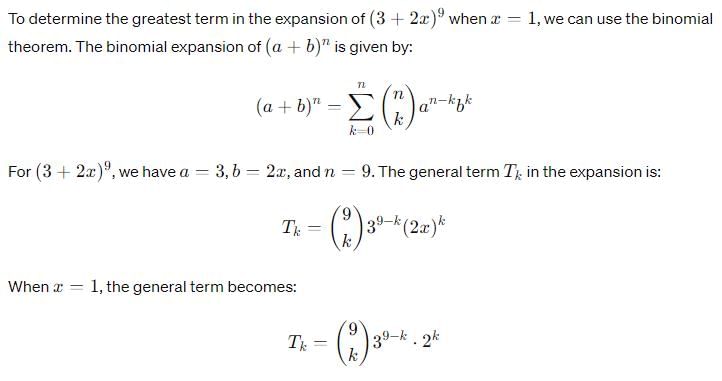


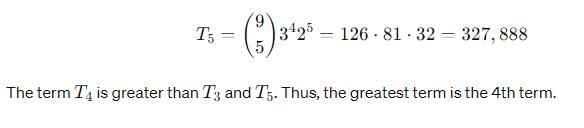

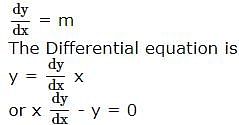
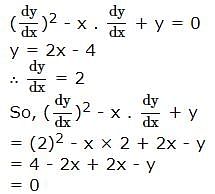
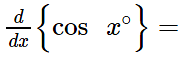
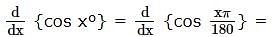
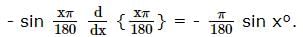
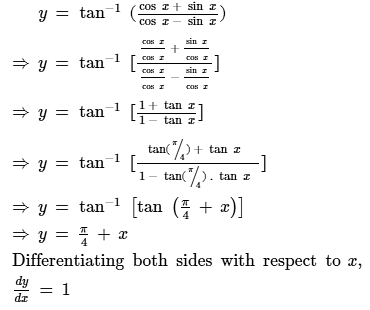



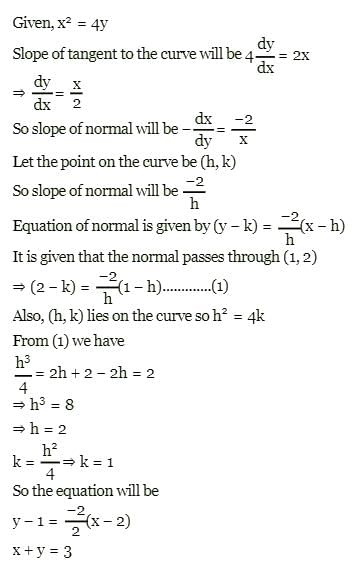
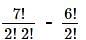 = 1260 - 360 = 900
= 1260 - 360 = 900














