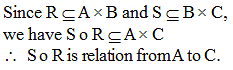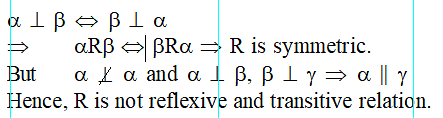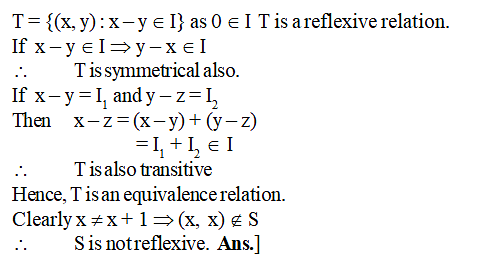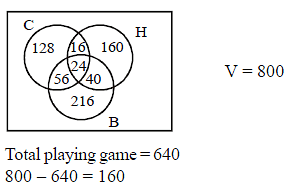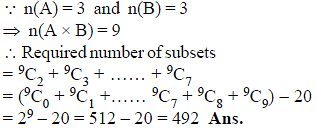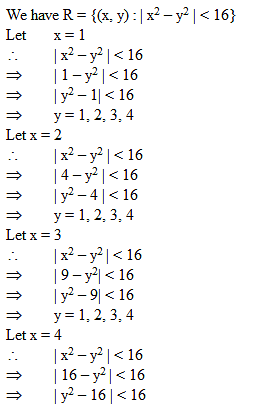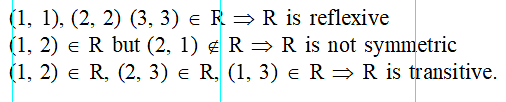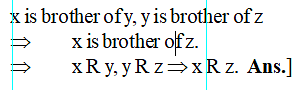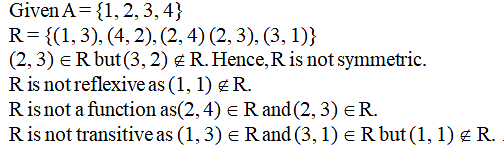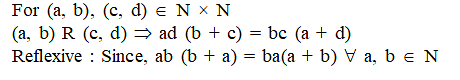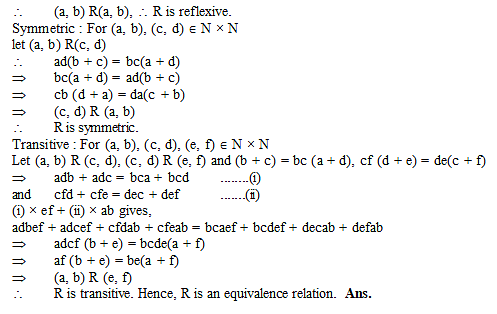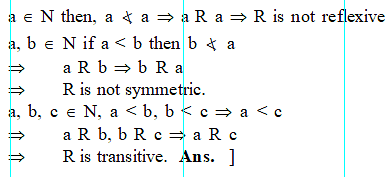Sets, Relations and Functions - 2 - JEE MCQ
30 Questions MCQ Test Mathematics (Maths) for JEE Main & Advanced - Sets, Relations and Functions - 2
Let A = {1, 2, 3, 4}, and let R = {(2, 2), (3, 3), (4, 4), (1, 2)} be a relation on A. Then R is-
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a relation on the set A = {1, 2, 3, 4}. The relation R is
If R is relation from a set A to a set B and S is a relation from B to C, then the relation S o R
A relation R is defined from {2, 3, 4, 5} to {3, 6, 7, 10} by xRy ⇔ x is relatively prime to y. Then domain of R is
Let R be the real line. Consider the following subsets of the plane R × R :
S = {(x, y): y = x + 1 and 0 < x < 2}
T = {(x, y) : x – y is an integer}.
Which one of the following is true ?
Let R and S be two equivalence relations on a set A. Then
Let R be a relation on the set N of natural numbers defined by nRm Û n is a factor of m (i.e. n | m). Then R is
Let R and S be two non-void relations on a set A. Which of the following statements is false?
Let W denote the words in the English dictionary. Define the relation R by : R = {(x, y) ∈ W × W | the words x and y have at least one letter in common}. Then R is –
If R be a relation < from A = {1, 2, 3, 4} to B = {1, 3, 5} i.e. (a, b) ∈ R ⇔ a < b, then RoR–1 is
Let R {(3, 3), (6, 6), (9, 9), (12, 12) (6, 12) (3, 9) (3, 12), (3, 6)} be a relation on the set A = {3, 6, 9, 12}. The relation is -
Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball of the total , 64 played both basketball and hockey, 80 played cricket and basketball and 40 played cricket and hockey, 24 played all the three games. The number of boys who play only cricket is
The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on the set A = {1, 2, 3} is -
Let A and B be two sets each containing three elements then number of subsets of A × B, each having at least two and at most 7 elements, is equal to
Let R be a relation defined in the set of real numbers by a R b ⇔ 1 + ab > 0. Then R is-
The relation R defined in A = {1, 2, 3} by aRb if |a2 – b2| ≤ 5. Which of the following is false
Let W denote the words in the English dictionary. Define the relation R by
R = {(x,y) ∈ W × W | the words x and y have atleast one letter in common |
Then R is
The relation R defined on the set A = {1, 2, 3, 4, 5} by R = {(x, y) : | x2 – y2 | < 16} is given by
The relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on the set A = {1, 2, 3} is -
Let R : A → A, A is set of all children in a family such that x R ⇒ y x is brother of ‘y’ (where x, y ∈ A), then R is-
Let R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} be a releation on the set A = {1, 2, 3, 4}. The relation R is-
Let N denote the set of all natural numbers and R be the relation on N × N defined by (a, b) R (c, d) if ad (b + c) = bc (a + d), then R is-
For real numbers x and y, we write x R y ⇔ x – y + √2 is an irrational number. Then the relation R is -
An integer m is said to be related to another integer n if m is a multiple of n. Then, the relation is
Given the relation R = {(2, 3), (3,4)} on the set {2, 3, 4}. The number of minimum number of ordered pairs to be added to R so that R is reflexive and symmetric –
The relation "less than" in the set of natural numbers is
The minimum number of elements that must be added to the relation R = {(1, 2), (2, 3)} on the set {1,2,3}, so that it is equivalence is-
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|