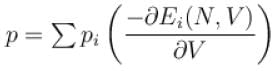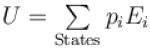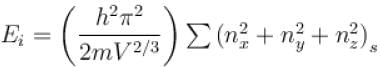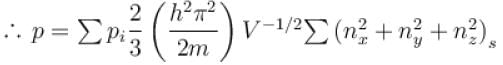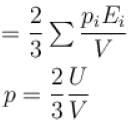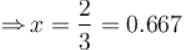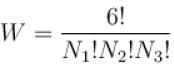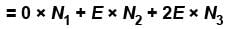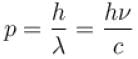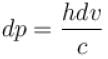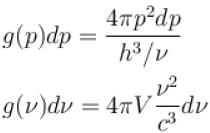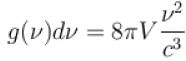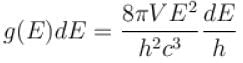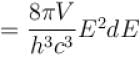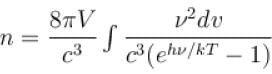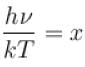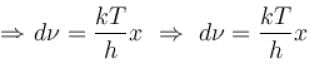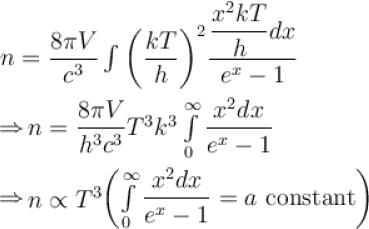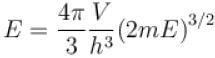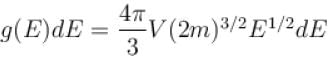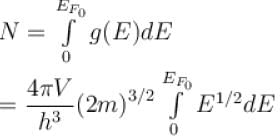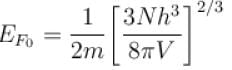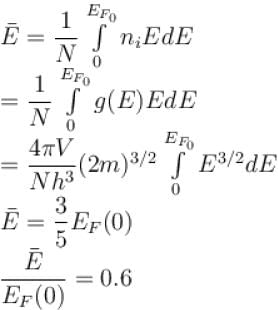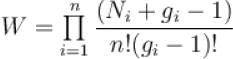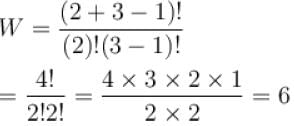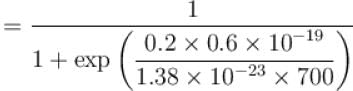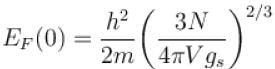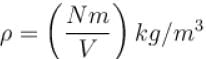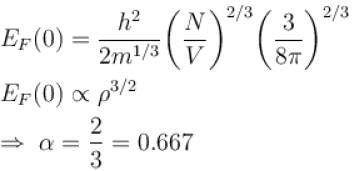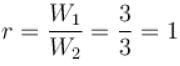Statistical Physics NAT Level – 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Statistical Physics NAT Level – 2
The pressure for a non-interacting Fermi gas with internal energy U at temperature T is given as 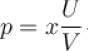 . Find value of x?
. Find value of x?
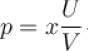 . Find value of x?
. Find value of x?During compression of a spring, the work done is 10 kJ and 2 kJ escaped to the surrounding as heat. The change in internal energy ∆U (in kJ) is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
According to Fermi-Dirac statistic the number of particles in a phase cell is.
Six distinguishable particles are distributed over three non-degenerate levels of energies 0, E and 2E. The total energy of the distribution for which the probability is a maximum is (in terms of E)?
Consider a radiation cavity of volume V at temperature T. The average number of photons in equilibrium is proportional to Tα , Find α?
Ratio is average energy of an electron in a metal at T = 0 to the Fermi energy at T = 0 is.
Consider a system of 2 identical particles each of which can be in any one of the 3 single particles states. The number states of the systems are possible in B-E statistics?
The probability that a state which is 0.2eV above the Fermi energy in metal atom at 700K is.
The Fermi energy of a free electron gas depends on the electron density ρ as 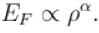 Find the value of α?
Find the value of α?
In a system of particles, each particles can be in any one of three possible quantum states. The ratio of the probability that the two particles occupy the same state to the probability that the two particle occupy different state for B-E statistics is.