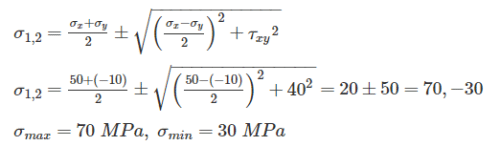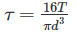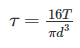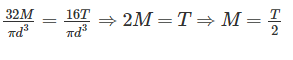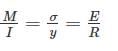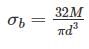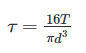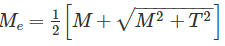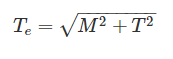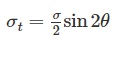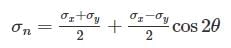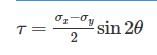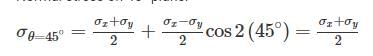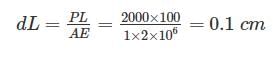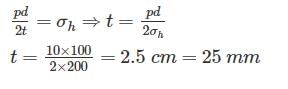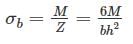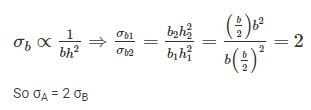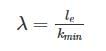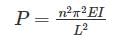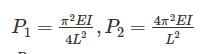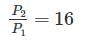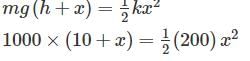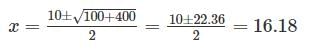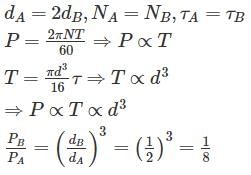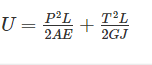Strength of Materials - 1 - Mechanical Engineering MCQ
20 Questions MCQ Test - Strength of Materials - 1
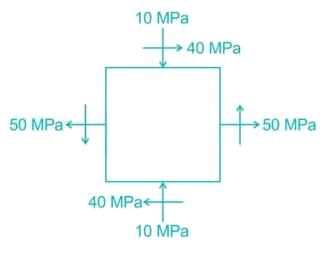
For the state of plane stress shown in the figure, the maximum and minimum principal stresses are:

Bending moment M and torque T is applied on a solid circular shaft. If the maximum bending stress equals to maximum shear stress developed, then M is equal to
When bending moment M and torque T is applied on a shaft then equivalent torque is
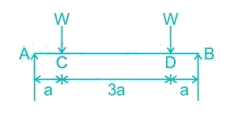
The bending moment diagram for the case shown below in Figure will be:
If a prismatic bar be subjected to an axial tensile stress σ, then shear stress induced on a plane inclined at θ with the axis will be
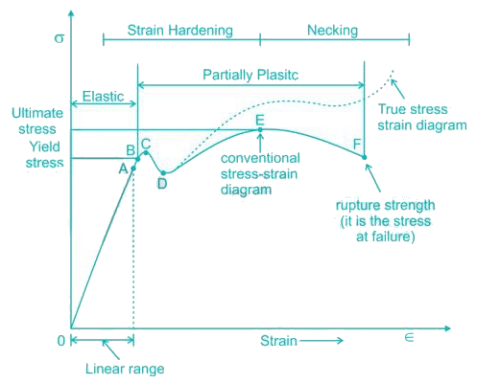
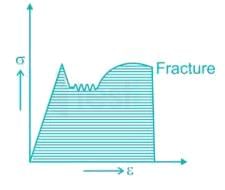
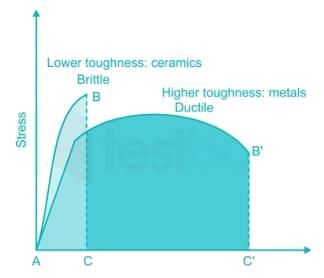
Select the proper sequence
1. Proportional Limit 2. Elastic limit
3. Yielding 4. Failure
In the case of bi-axial state of normal stresses, the normal stress on 45° plane is equal to
The temperature stress is a function of
1. Coefficient of linear expansion
2. Temperature rise
3. Modulus of elasticity
A steel rod of 1 sq. cm. cross sectional area is 100 cm long and has a Young’s modulus of elasticity 2 × 106 kgf/cm2. It is subjected to an axial pull of 2000 kgf. The elongation of the rod will be
Assume that young's modulus of a wire of length L and radius 'r' is Y. If length is reduced to L/2 and radius r/2 then what will be its young's modulus?
Circumferential and longitudinal strains in cylindrical boiler under internal steam pressure, are ε1 and ε2 respectively. Change in volume of the boiler cylinder per unit volume will be
A metal pipe of 1 m diameter contains a fluid having a pressure of 10 kgf/cm2. If the permissible tensile stress in the metal is 200 kgf/cm2, then the thickness of the metal required for making the pipe would be
Hoops stress and longitudinal stress in a boiler shell under internal pressure are 100 MN/m2 and 50 MN/m2 respectively. Young’s modulus of elasticity and Poisson’s ratio of the shell material are 200 GN/m2 and 0.3 respectively. The hoop strain in boiler shell is
A beam cross-section is used in two different orientations as shown in figure given below:

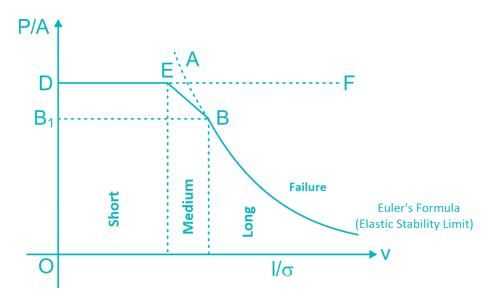
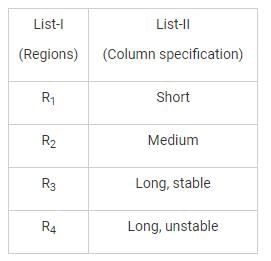
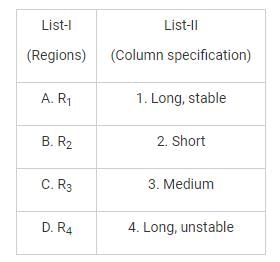
The curve ABC is the Euler’s curve for stability of column. The horizontal line DEF is the strength limit. With reference to this figure Match List-I and select the correct answer using the codes below the lines

With one fixed end and other free end, a column of length L buckles at load, P1. Another column of same length and same cross-section fixed at both ends buckles at load P2. Value of P2/P1 is
A body having weight of 1000 N is dropped form a height of 10 cm over a close-coiled helical spring of stiffness 200 N/cm. The resulting deflection of spring is nearly
The diameter of shaft A is twice the diameter of shaft B and both are made of the same material. Assuming both the shafts to rotate at the same speed, the maximum power transmitted by B is
A bar having length L and uniform cross-section with area A is subjected to both tensile force P and torque T. If G is the shear modulus and E is the Young’s modulus, the internal strain energy stored in the bar is
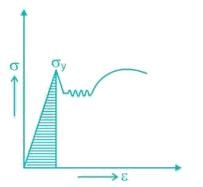
Resilience for mild steel under uni-axial tensile loading is given by the shaded portion of the stress-strain diagram as shown in