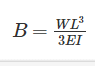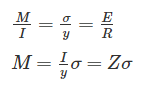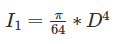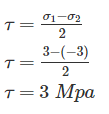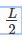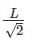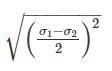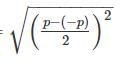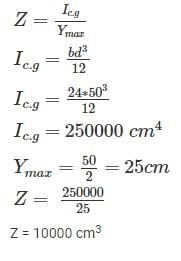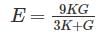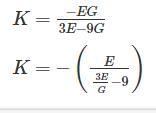Strength of Materials - 3 - Mechanical Engineering MCQ
20 Questions MCQ Test SSC JE Mechanical Mock Test Series 2026 - Strength of Materials - 3
The resistance per unit area, offered by a body against deformation is known as:
Which of the following load does not act on the considerable length of the beam?
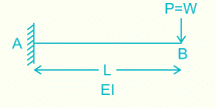
The maximum deflection due to a load W at the free end of a cantilever of length L and having flexural rigidity EI is
If section modulus of a beam is increased, the bending stress in the beam will:
When the shear force diagram is a parabolic curve between two points, it indicates that there is a
Mohr’s circle can be used to determine the following stress on an inclined surface:
A. Principal stress
B. Normal stress
C. Tangential stress
D. Maximum shear stress
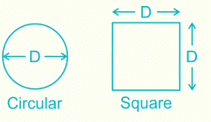
The ratio of moment of inertia of circular plate to that of square plate of equal depth is:
The major and minor principal stresses at a point are 3Mpa and -3Mpa respectively. The maximum shear stress at the point is
The equivalent length of a column of length L having one end fixed and the other end free is
The radius of Mohr’s circle for two equal and unlike principal stresses of magnitude “p” is:
A rectangular beam is 24 cm wide and 50 cm deep, its section modulus is given by:
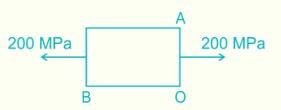
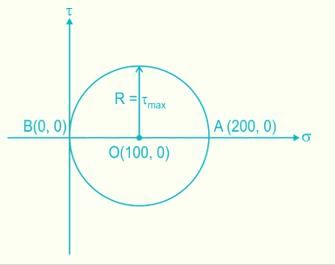
The stress at a point in a bar is 200 MPa tensile. Determine the intensity of maximum shear stress in the material.
The correct relation between Modulus of elasticity (E), Shear Modulus (G) and Bulk modulus (K) is:
The total area under the stress-strain curve of a mild steel specimen tested up to failure under tension is a measure of its:
The neutral axis of a beam is subjected to _________ stress.
|
3 videos|1 docs|55 tests
|