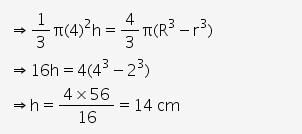Surface Area & Volumes - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ
25 Questions MCQ Test - Surface Area & Volumes - Olympiad Level MCQ, Class 9 Mathematics
Ratio of lateral surface areas of two cylinders with equal heights is :
Ratio of volumes of two cylinders with equal radii are :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The lateral surface area of cylinder is 176 cm2 and base area 38.5 cm2. The its volume is ____.
A cylinderical vessel contains 49.896 litres of liquid. cost of painting its CSA at 2 paise/sq cm is Rs. 95.04.
Then its total surface area is ______.
The area of the base of a cone is 616 sq cm. Its height is 48 cm. Then its total surface area is ____.
A vessel is in conical shape. If its volume is 33.264 litres and height is 72 cm, the cost of repairing its CSA
at Rs. 12/sq m is :
From a circle of radius 15 cm a sector with 216° angle is cut out and its bounding radii are bent so as to
form a cone. Then its volume is :
A hemispherical bowl is made of steel of 0.25 cm thickness. The inner radius of the bowl is 5 cm. The volume
of steel used is _____.
A cuboidal metal of dimensions 44 cm × 30 cm × 15 cm was melted and case into a cylinder of height 28
cm. Its radius is _____.
A piece of metal pipe is 77 cm long with inside diameter of the cross section as 4 cm. If teh outer diameter is
4.5 cm and the metal weighs 8 gm/cu cm, the weight of pipe is _____.
A circus tent is in the form of a cone over a cylinder. The diameter of the base is 9 m, the height of cylindrical
part is 4.8 m and the total height of the tent is 10.8 m. The canvas required for the tent is _____.
The diameter of a copper sphere is 6 cm. It is beaten and drawn into a wire of diameter 0.2 cm. The length
of wire is _____.
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base
diameter 8 cm. Find the height of the cone.
The radius of the cylinder whose lateral surface area is 704 cm2 and height 8 cm is :
The ratio of the volume and surface area of a sphere of unit radius :
Two identical right circular cones each of height 2 cm are placed as showin in diagram (each is vertical, apex downward). At the start, the upper cone is full of water and lower cone is empty.
Then water drips down through a hole in the apex of upper cone into the lower cone. The height of water in the lower cone at the moment when height of water in uper cone is 1 cm is :
A sphere and a cube are of the same height. The ratio of their volume is :
The largest sphere is cut off from a cube of side 5 cm. The volume of the sphere will be :
The edge of a cube is 20 cm. How many small cubes of 5 cm edge can be formed from this cube?
In the figure below, RSTV is a square inscribed in a circle with centre O and radius r. The total area of shaded region is :
Correct the perimeter of the figure given below to one decimal place :
A hollow spherical ball whose inner radius is 4 cm is full of water. Half of the water is transferred to a conical
cup and it completely filled' he cup. If the height of the cup is 2 cm, then the radius of the base of cone, in cm is :
The largest volume of a cube that can be enclosed in a sphere of diameter 2 cm is (in cm3).
Each side of a cube is increased by 50%. Then the surface area of the cube increases by :
The number of surfaces in right circular cylinder is :
Top Courses for Class 9
Important Questions for Surface Area & Volumes - Olympiad Level MCQ, Class 9 Mathematics
Surface Area & Volumes - Olympiad Level MCQ, Class 9 Mathematics
Online Tests for Surface Area & Volumes - Olympiad Level MCQ, Class 9 Mathematics
|
© EduRev
|
Education Revolution
|
|
