Test (With calculator) - 3 - SAT MCQ
15 Questions MCQ Test Digital SAT Mock Test Series 2024 - Test (With calculator) - 3

The data in the table above were produced by a sleep researcher studying the number of dreams people recall when asked to record their dreams for one week. Group X consisted of 100 people who observed early bedtimes, and Group Y consisted of 100 people who observed later bedtimes. If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y?

The data in the table above were produced by a sleep researcher studying the number of dreams people recall when asked to record their dreams for one week. Group X consisted of 100 people who observed early bedtimes, and Group Y consisted of 100 people who observed later bedtimes. If a person is chosen at random from those who recalled at least 1 dream, what is the probability that the person belonged to Group Y?
Question refer to the following information.
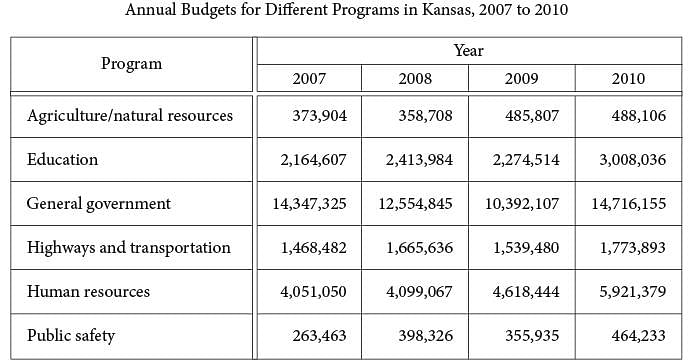
The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
Which of the following best approximates the average rate of change in the annual budget for agriculture/natural resources in Kansas from 2008 to 2010?

The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Question refer to the following information.

The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
Of the following, which program’s ratio of its 2007 budget to its 2010 budget is closest to the human resources program’s ratio of its 2007 budget to its 2010 budget?

The table above lists the annual budget, in thousands of dollars, for each of six different state programs in Kansas from 2007 to 2010.
Which of the following is an equation of a circle in the xy-plane with center (0, 4) and a radius with endpoint (4/3, 5)?
h = − 4.9t2 + 25t
The equation above expresses the approximate height h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?
Katarina is a botanist studying the production of pears by two types of pear trees. She noticed that Type A trees produced 20 percent more pears than Type B trees did. Based on Katarina’s observation, if the Type A trees produced 144 pears, how many pears did the Type B trees produce?
A square field measures 10 meters by 10 meters.
Ten students each mark off a randomly selected region of the field; each region is square and has side lengths of 1 meter, and no two regions overlap. The students count the earthworms contained in the soil to a depth of 5 centimeters beneath the ground’s surface in each region. The results are shown in the table below.
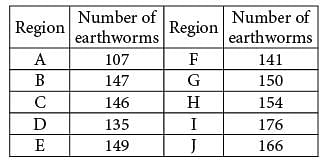
Which of the following is a reasonable approximation of the number of earthworms to a depth of 5 centimeters beneath the ground’s surface in the entire field?
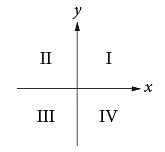
If the system of inequalities y ≥ 2x + 1 and 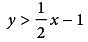 is graphed in the xy-plane above, which quadrant contains no solutions to the system?
is graphed in the xy-plane above, which quadrant contains no solutions to the system?
For a polynomial p(x) , the value of p(3) is −2. Which of the following must be true about p(x)?
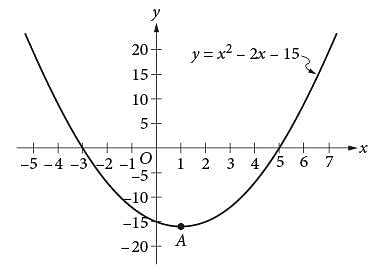
Which of the following is an equivalent form of the equation of the graph shown in the xy-plane above, from which the coordinates of vertex A can be identified as constants in the equation?
Wyatt can husk at least 12 dozen ears of corn per hour and at most 18 dozen ears of corn per hour.
Based on this information, what is a possible amount of time, in hours, that it could take Wyatt to husk 72 dozen ears of corn?
The posted weight limit for a covered wooden bridge in Pennsylvania is 6000 pounds. A delivery truck that is carrying x identical boxes each weighing 14 pounds will pass over the bridge. If the combined weight of the empty delivery truck and its driver is 4500 pounds, what is the maximum possible value for x that will keep the combined weight of the truck, driver, and boxes below the bridge’s posted weight limit?
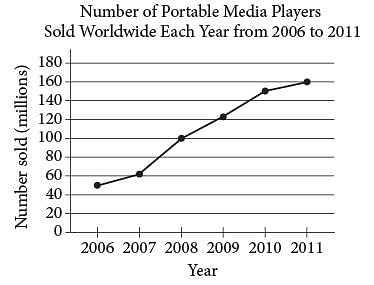
According to the line graph above, the number of portable media players sold in 2008 is what fraction of the number sold in 2011?
A local television station sells time slots for programs in 30-minute intervals. If the station operates 24 hours per day, every day of the week, what is the total number of 30-minute time slots the station can sell for Tuesday and Wednesday?
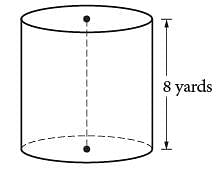
A dairy farmer uses a storage silo that is in the shape of the right circular cylinder above. If the volume of the silo is 72π cubic yards, what is the diameter of the base of the cylinder, in yards?
|
8 docs|22 tests
|


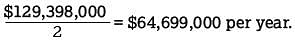 . Of the options given, this average rate of change is closest to $65,000,000 per year.
. Of the options given, this average rate of change is closest to $65,000,000 per year.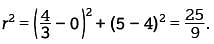 Therefore, an equation of the given circle is
Therefore, an equation of the given circle is 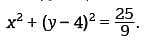
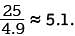 The time t = 0 seconds corresponds to the time the ball is launched from the ground, and the time t ≈ 5.1 seconds corresponds to the time after launch that the ball hits the ground. Of the given choices, 5.0 seconds is closest to 5.1 seconds, so the ball returns to the ground approximately 5.0 seconds after it is launched.
The time t = 0 seconds corresponds to the time the ball is launched from the ground, and the time t ≈ 5.1 seconds corresponds to the time after launch that the ball hits the ground. Of the given choices, 5.0 seconds is closest to 5.1 seconds, so the ball returns to the ground approximately 5.0 seconds after it is launched.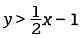 drawing a dashed line through the y-intercept (0, -1) and the point (2, 0), as shown. The solutions to this inequality are all points above this dashed line.
drawing a dashed line through the y-intercept (0, -1) and the point (2, 0), as shown. The solutions to this inequality are all points above this dashed line.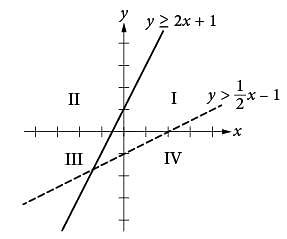
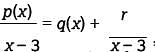 where q(x) is a polynomial and r is the remainder. Since x - 3 is a degree 1 polynomial, the remainder is a real number. Hence, p(x) can be written as p(x) = (x - 3)q(x) + r, where r is a real number. It is given that p(3) = -2 so it must be true that -2 = p (3) = (3 -3) q (3) + r = (0)q (3) + r = r. Therefore, the remainder when p(x) is divided by x - 3 is -2.
where q(x) is a polynomial and r is the remainder. Since x - 3 is a degree 1 polynomial, the remainder is a real number. Hence, p(x) can be written as p(x) = (x - 3)q(x) + r, where r is a real number. It is given that p(3) = -2 so it must be true that -2 = p (3) = (3 -3) q (3) + r = (0)q (3) + r = r. Therefore, the remainder when p(x) is divided by x - 3 is -2.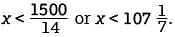 Since the number of packages must be an integer, the maximum possible value for x that will keep the combined weight of the truck, its driver, and the x identical boxes below the bridge’s posted weight limit is 107.
Since the number of packages must be an integer, the maximum possible value for x that will keep the combined weight of the truck, its driver, and the x identical boxes below the bridge’s posted weight limit is 107.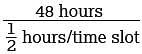 = 96 time slots of 30 minutes for the station to sell on Tuesday and Wednesday.
= 96 time slots of 30 minutes for the station to sell on Tuesday and Wednesday.














