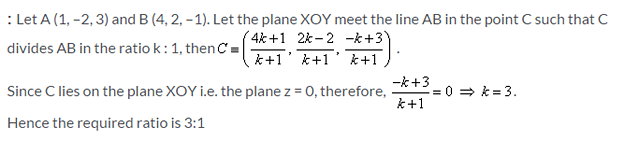Test: 3-D Geometry: Section Formula(12 Dec) - JEE MCQ
10 Questions MCQ Test Daily Test for JEE Preparation - Test: 3-D Geometry: Section Formula(12 Dec)
The coordinates of the centroid of a triangle whose vertices are (2, –1, 6), (3, 3, –2) and (–2, 1, –1) are:
The ratio, in which YZ-plane divides the line joining (2, 4, 5) and (3, 5, 7) is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
Three vertices of a parallelogram PQRS are P(3, – 1, 2), Q (1, 2, – 4) and R (- 1, 1, 2). Find the coordinates of the fourth vertex.
A point R with x-coordinate 1 lies on the line segment joining the points P(-2, 3,5) and Q (7, 0, -1). The coordinates of the point R are
If the origin is the centroid of the triangle ABC with vertices A (2a, 14, 6), B (8, 3b, -10) and C(-4, 2, 2c), then the values of a and c are.
If the origin is the centroid of the triangle PQR with vertices P(2a, 2, 6), Q(-4, 3b, -10) and (8, 14, 2c), then the values of a, b and c are:
The ratio in which the join of points (1, –2, 3) and (4, 2, –1) is divided by XOY plane is:
The coordinates of the point R which divides the line segment joining two points P (x1, y1, z1) and Q (x2, y2, z2) externally in the ratio m : n are given by
The ratio in which the line joining the points (1, 2, 3) and (-3.4, -5) is divided by the xy-plane is:
|
360 tests
|