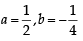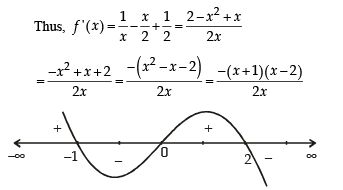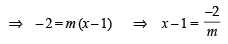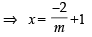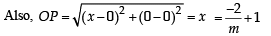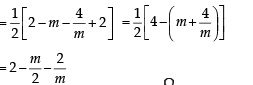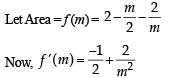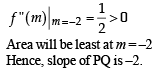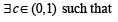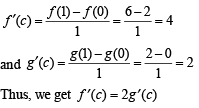Test: 35 Year JEE Previous Year Questions: Applications of Derivatives - JEE MCQ
30 Questions MCQ Test - Test: 35 Year JEE Previous Year Questions: Applications of Derivatives
The maximum distance from origin of a point on the curve
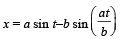
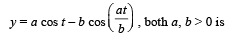
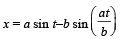
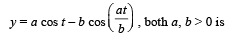
If 2a + 3b + 6c = 0, (a, b, c ∈ R) then the quadratic equation ax2 + bx + c = 0 has
If th e function f ( x) = 2x3 - 9ax2 + 12a2x+1 , whe re a > 0 , attains its maximum and minimum at p and q respectively such that p 2 = q , then a equals
A point on th e parabola y2 = 18x at which the ordinate increases at twice the rate of the abscissa is
A function y = f (x) h as a second or der der iva tive f "( x) = 6(x- 1). If its graph passes through the point (2,1) and at that point the tangent to the graph is y = 3x – 5, then the function is
The normal to the curve x = a(1 + cosθ), y = a sinθ at ‘θ’ always passes through the fixed point
If 2a + 3b + 6c = 0, then at least one root of the equation ax2 + bx +c= 0 lies in the interval
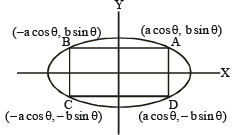
Area of the greatest rectangle that can be inscribed in the ellipse 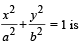
The normal to the curve x = a (cos θ + θ sin θ), y = a (sin θ – θ cos θ) at any point θ ' is such that
A spherical iron ball 10 cm in radius is coated with a layer of ice of uniform thickness that melts at a rate of 50 cm 3/min.
When the thickness of ice is 5 cm,then the rate at which the thickness of ice decreases is
If the equation 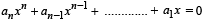
 has a positive root x = a , then the equation
has a positive root x = a , then the equation 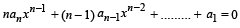 has a positive root, which is
has a positive root, which is
The function 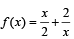 has a local minimum at
has a local minimum at
A triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. The two sides having fence are of same length x. The maximum area enclosed by the park is
A value of c for which conclusion of Mean Value Theorem holds for the function f (x) = loge x on the interval [1, 3] is
The function f (x) = tan–1(sin x + cos x) is an increasing function in
If p and q are positive real numbers such that p2 + q2 = 1, then the maximum value of (p + q) is
Suppose the cubic x3 – px + q has three distinct real roots where p > 0 and q > 0. Then which one of the following holds?
How many real solutions does the equation
x7 + 14x5 + 16x3 + 30x – 560 = 0 have?
Let f (x) = x | x | and g (x) = sin x.
Statement-1 : gof is differentiable at x = 0 and its derivative is continuous at that point.
Statement-2 : gof is twice differentiable at x = 0.
Given P(x) = x4 + ax3 + bx2 + cx + d such that x = 0 is the only real root of P' (x) = 0. If P(–1) < P(1), then in the interval [ –1, 1] :
The equation of the tangent to the curve 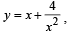 that is parallel to the x-axis, is
that is parallel to the x-axis, is
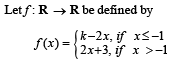
If f has a local minimum at x = – 1 , then a possible value of k is
Let f : R → R be a continuous function defined by
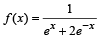
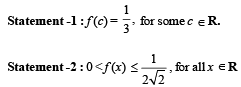
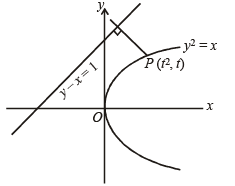
The shortest distance between line y – x = 1 and curve x = y2 is
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is :
Let a, b ∈ R be such that the function f given by f (x) = ln |x|+ bx2 + ax, x ≠ 0 has extreme values at x = –1 and x = 2
Statement-1 : f has local maximum at x = –1 and at x = 2.
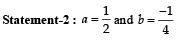
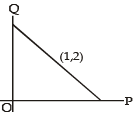
A line is drawn through the point (1,2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is :
The intercepts on x-axis made by tangents to the curve, 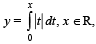 which are parallel to the line y = 2x, are equal to :
which are parallel to the line y = 2x, are equal to :
If f and g are differentiable functions in [0, 1] satisfying f (0) = 2 = g(1), g(0) = 0 and f (1) = 6, then for some c ∈[0,1]


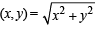
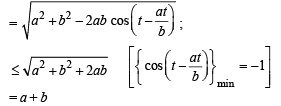
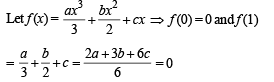

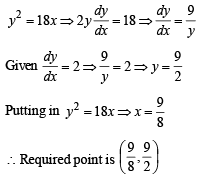
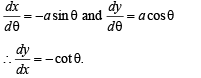
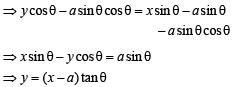
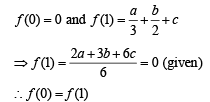
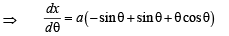
 .....(1)
.....(1)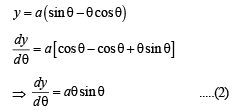

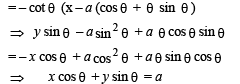
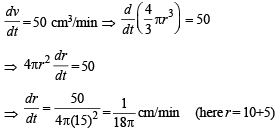
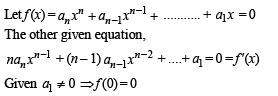
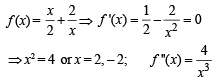
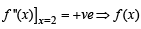 has local min at x = 2.
has local min at x = 2.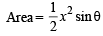
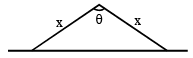
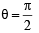
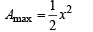
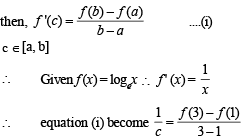

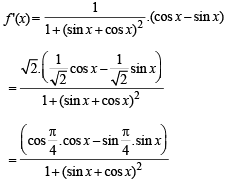
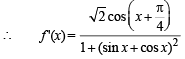
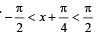
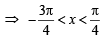
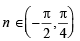
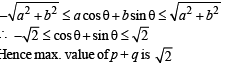
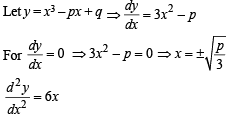
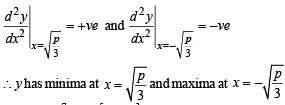
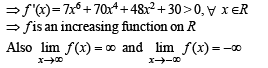
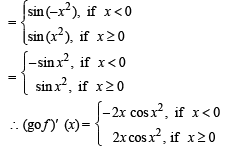


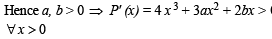
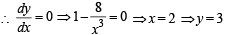
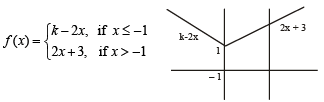
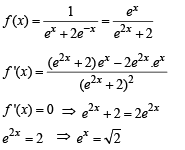
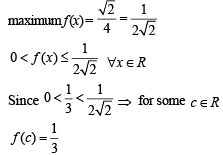
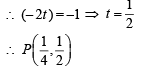
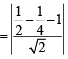
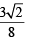

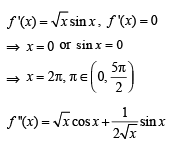
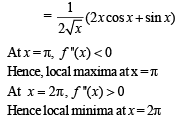
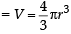
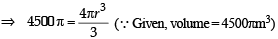
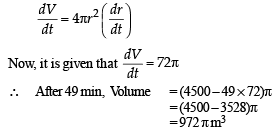
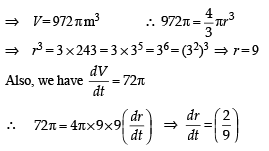
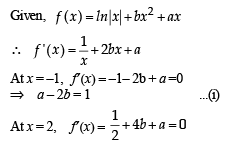
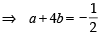 ...(ii)
...(ii)