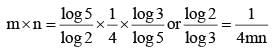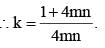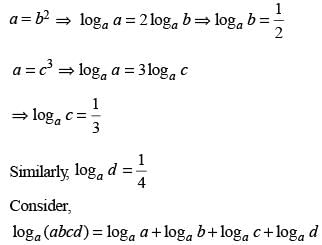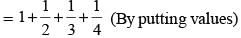Test: Algebra - 2 - CAT MCQ
25 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Algebra - 2
Let x and y be positive real numbers such that
log5 (x + y) + log5 (x – y) = 3, and log2 y – log2 x = 1 – log2 3. Then xy equals
(2019)
log5 (x + y) + log5 (x – y) = 3, and log2 y – log2 x = 1 – log2 3. Then xy equals
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the population of a town is p in the beginning of any year then it becomes 3 + 2p in the beginning of the next year. If the population in the beginning of 2019 is 1000, then the population in the beginning of 2034 will be
(2019)
If (2n + 1) + (2n + 3) + (2n + 5) + ... + (2n + 47) = 5280, then what is the value of 1 + 2 + 3 + ... + n?
(2019)
Let A be a real number. Then the roots of the equation x2 – 4x – log2A = 0 are real and distinct if and only if
(2019)
Let a1, a2, ... be integers such that a1 – a2 + a3 – a4 + ... + (–1)n–1. an = n, for all n ≥ 1.
Then a51 + a52 + . . . + a1023 equals
(2019)
Let x, y, z be three positive real numbers in a geometric progression such that x < y < z. If 5x, 16y, and 12z are in an arithmetic progression then the common ratio of the geometric progression is
(2018)
If x is a positive quantity such that 2x = 3log 52, then × is equal to
(2018)
Given that X2018Y2017 = 1/2 and X2016Y2019 = 8, the value of x2 + y3 is
(2018)
If log2(5 + log3 a) = 3 and log5(4a + 12 + log2 b) = 3, then a + b is equal to
(2018)
Let a1, a2...., a2n be an arithmetic progression with a1 = 3 and a2 = 7. If a1 + a2 + ... + a3n = 1830, then what is the smallest positive integer m such that m(a1 + a2 + ... + an) > 1830?
(2017)
If the square of the 7th term of an arithmetic progression with positive common difference equals the product of the 3rd and 17th terms, then the ratio of the first term to the common difference is
(2017)
Two positive real numbers, a and b, are expressed as the sum of m positive real numbers and n positive real numbers respectively as follows:
a = s1 + s2 +…+ sm and b = t1 + t2 +…+ tn
If [a] = [s1] + [s2] +…+ [sm] + 4 and [b] = [t1 ] + [t2 ] +…+ [tn] + 3,
Where [x] denotes the greatest integer less than or equal to x, what is the minimum possible value of m + n?
(2016)
P1, P2, P3, ..., P11 are 11 friends. The number of balls with P1 through P11 in that order is in an Arithmetic Progression. If the sum of the number of balls with P1, P3, P5, P7, P9 and P11 is 72, what is the number of balls with P1, P6 and P11 put together?
(2014)
If log32, log3(2x – 5) and log3 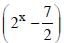 are in Arithmetic Progression, then x is equal to
are in Arithmetic Progression, then x is equal to
(2014)
A ray of light along the line  gets reflected on the x-axis to become a ray along the line
gets reflected on the x-axis to become a ray along the line
(2014)
If 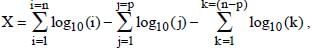 where p ≤ n, then the maximum value of X for n = 8 is :
where p ≤ n, then the maximum value of X for n = 8 is :
(2014)
If x + y = 1, then what is the value of (x3 + y3 + 3xy)?
(2012)
If log165 = m and log53 = n, then what is the value of log36 in terms of ‘m’ and ‘n’?
(2011)
If a = b2 = c3 = d4 then the value of loga (abcd) would be :
(2010)
|
43 docs|31 tests
|
|
43 docs|31 tests
|


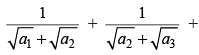
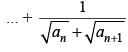 is equal to
is equal to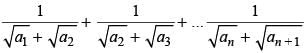
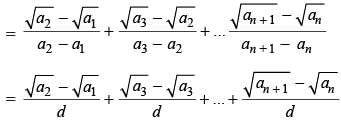
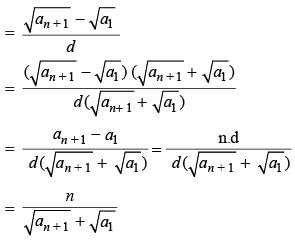
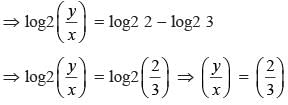
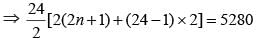
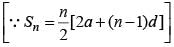
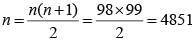

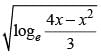 is a real number if and only if
is a real number if and only if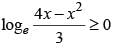
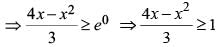
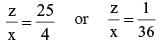
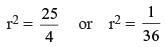 [r is the common ratio]
[r is the common ratio]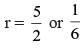
 because x, y, z > 0 and x < y < z
because x, y, z > 0 and x < y < z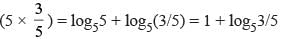
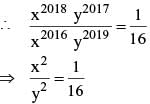
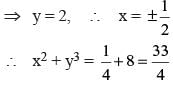
 is equal to
is equal to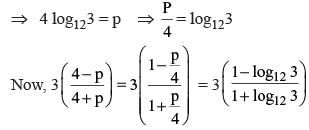

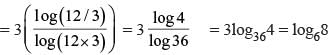
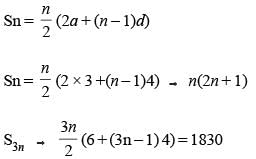
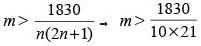
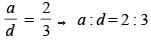
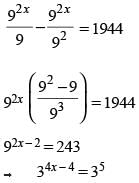
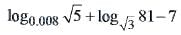
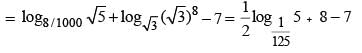
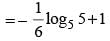
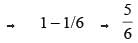
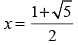 (∵ x > 0)
(∵ x > 0)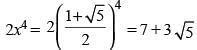
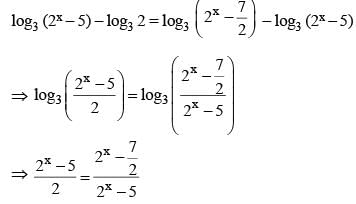

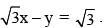
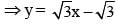
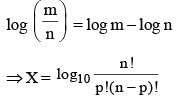
 is maximum.
is maximum.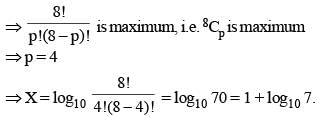
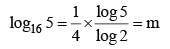 ...(i)
...(i) ...(ii)
...(ii)