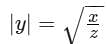Test: Algebra - GMAT MCQ
10 Questions MCQ Test Practice Questions for GMAT - Test: Algebra
If abc = b3 , which of the following must be true?
I. ac = b2
II. b = 0
III. ac = 1
II. b = 0
III. ac = 1
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Both roots of the quadratic equation x2 − 63 ∗ x + k = 0 are prime numbers. The number of possible values of k are?
A manufacturer produces a certain men's athletic shoe in integer sizes from 8 to 17. For this particular shoe, each unit increase in size corresponds to a 1/4-inch increase in the length of the shoe. If the largest size of this shoe is 20% longer than the smallest size, how long, in inches, is the shoe in size 15?
The quadratic equation x2 + bx + c = 0 has two roots 4a and 3a, where a is an integer. Which of the following is a possible value of b2 +c ?
If the coordinates of point A are (2,2) and the coordinates of point B are (0,-2), what is the equation of the perpendicular bisector of line segment AB?
A, B and C are partners. A receives 2/3 of profit, B and C dividing the remaining profit equally. A's income is increased by $400 when the rate of profit rises from 5% to 7%. Find the profit of B
If x and z are positive constants, for how many values of y is x(y)2 = z(y)4?
If f(x) = 3x2 - tx + 5 is tangents to x-axis, what is the value of a positive number t?
|
18 docs|139 tests
|