Test: Algorithm Analysis & Asymptotic Notation- 1 - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Algorithm Analysis & Asymptotic Notation- 1
The order of an algorithm that finds whether a given Boolean function of ‘n’ variables, produces a 1 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The order of the binary search algorithm is
For merging two sorted lists of sizes m and n into a sorted list of size m + n. Find out the time complexity of this merging process.
A machine needs a minimum of 100 sec to sort 1000 names by quick sort. The minimum time needed to sort 100 names will be approximately
A machine took 200 sec to sort 200 names, using bubble sort. In 800 sec, it can approximately sort
Unrestricted use of goto is harmful, because it
The recurrence relation that arises in relation with the complexity of binary search is
Consider the following two functions:
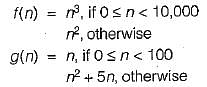
Which of the following is/are true?
1. f(n) is O(n3)
2. g(n) is O (n3)
3. 0(f(n)) is same as O(g(n))
4. g(n) is O{n2)
Suppose f, g, h, k : N→ N.
If f = 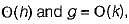 then
then
|
63 videos|7 docs|165 tests
|
|
63 videos|7 docs|165 tests
|


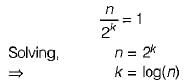
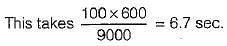
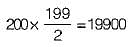 comparisons. The time needed for 1 comparison is 200 sec (approximately). In 800 sec it can make 80,000 comparisons. We have to find n, such that
comparisons. The time needed for 1 comparison is 200 sec (approximately). In 800 sec it can make 80,000 comparisons. We have to find n, such that 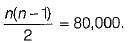
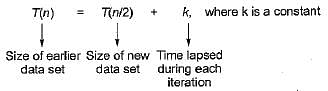
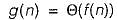 in case of otherwise From the above two equations the conclusion is O(f (n)) is same as O(g(m)) and g(n) and f(n) will be O(n2).
in case of otherwise From the above two equations the conclusion is O(f (n)) is same as O(g(m)) and g(n) and f(n) will be O(n2).