Test: Alternating Current - 2 - JEE MCQ
30 Questions MCQ Test - Test: Alternating Current - 2
In an ac circuit, peak value of voltage is 423 volts. Its effective voltage is
An ac circuit, the current is given by i = 4 sin (100pt + 30º) ampere. The current becomes maximum first time (after t = 0) at t equal to
The instantaneous value of current in an ac circuit is I = 2 sin (100pt + p/3) A. The current at the beginning (t = 0) will be
If instantaneous value of current is I = 10 sin (314 t) A, then the average current for the half cycle will be
In a circuit an a.c. current and a d, c. current are supplied together. The expression of the instantaneous current is given as i = 3 + 6 sin wt. Then the rms value of the current is
The emf and the current in a circuit are E = 12 sin (100pt) ; I = 4 sin (100pt + p / 3) then
If the frequency of alternating potential is 50Hz then the direction of potential, changes in one second by
The value of alternating e.m.f. is e = 500 sin 100pt , then the frequency of this potential in Hz is
The domestic power supply is at 220 volt. The amplitude of emf will be
The average value or alternating current for half cycle in terms of I0 is
Sinusoidal peak potential is 200 volt with frequency 50Hz. It is represented by the equation
The phase difference between the alternating current and voltage represented by the following equation I = I0 sin wt, E = E0 cos (wt + p / 3), will be
The inductive reactance of a coil is 1000W. If its self inductance and frequency both are increased two times then inductive reactance will be
In an L.C.R series circuit R = 1W, XL = 1000W and XC = 1000W. A source of 100 m.volt is connected in the circuit the current in the circuit is
A coil of inductance 0.1 H is connected to an alternating voltage generator of voltage E = 100 sin (100t) volt. The current flowing through the coil will be
Alternating current lead the applied e.m.f. by p/2 when the circuit consists of
A coil has reactance of 100W when frequency is 50Hz. If the frequency becomes 150Hz, then the reactance will be
A resistance of 50Ω, an inductance of 20/π henry and a capacitor of 5/π μF are connected in series with an A.C. source of 230 volt and 50Hz. The impedance of the circuit is
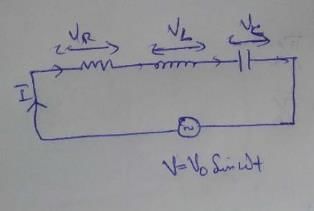
The potential difference between the ends of a resistance R is VR between the ends of capacitor is VC = 2VR and between the ends of inductance is VL = 3VR, then the alternating potential of the source in terms of VR will be
The percentage increase in the impedance of an ac circuit, when its power factor changes form 0.866 to 0.5 is (Resistance constant)
In a series resonant L_C_R circuit, if L is increased by 25% and C is decreased by 20%, then the resonant frequency will
Which of the following statements is correct for L_C_R series combination in the condition of resonance
An ac circuit resonates at a frequency of 10 kHz. If its frequency is increased to 11 kHz, then
In an ac circuit emf and current are E = 5 cos wt volt and I = 2 sin wt ampere respectively. The average power dissipated in this circuit will be
A choke coil of negligible resistance carries 5 mA current when it is operated at 220 V. The loss of power in the choke coil is –
In an A.C. circuit, a resistance of 3W, an inductance coil of 4W and a condenser of 8W are connected in series with an A.C. source of 50 volt (R.M.S.). The average power loss in the circuit will be
Two bulbs of 500 watt and 300 watt work on 200 volt r.m.s. the ratio of their resistances will be –
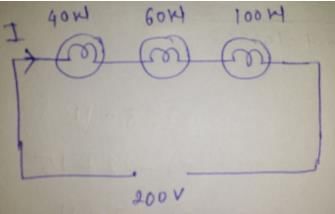
Three bulbs of 40, 60 and 100 watt are connected in series with the source of 200 volt. Then which of the bulb will be glowing the most –
Alternating current can not be measured by direct current meters, because –



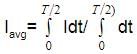 dt [ω=314, T=2π/ω=2π/314, T=π/157]
dt [ω=314, T=2π/ω=2π/314, T=π/157]