All Courses
Get the App Signup / Login
Sign in Open App
CAT Exam  >  CAT Tests  >  Daily Test for CAT Preparation  >  Test: Analytical Reasoning - 1(July 11) - CAT MCQ

Test: Analytical Reasoning - 1(July 11) - CAT MCQ


Test Description

10 Questions MCQ Test Daily Test for CAT Preparation - Test: Analytical Reasoning - 1(July 11)

Test: Analytical Reasoning - 1(July 11) for CAT 2024 is part of Daily Test for CAT Preparation preparation. The Test: Analytical Reasoning - 1(July 11) questions and answers have been prepared according to the CAT exam syllabus.The Test: Analytical Reasoning - 1(July 11) MCQs are made for CAT 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Analytical Reasoning - 1(July 11) below.
Solutions of Test: Analytical Reasoning - 1(July 11) questions in English are available as part of our Daily Test for CAT Preparation for CAT & Test: Analytical Reasoning - 1(July 11) solutions in Hindi for Daily Test for CAT Preparation course. Download more important topics, notes, lectures and mock test series for CAT Exam by signing up for free. Attempt Test: Analytical Reasoning - 1(July 11) | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study Daily Test for CAT Preparation for CAT Exam | Download free PDF with solutions
Test: Analytical Reasoning - 1(July 11) - Question 1
Save

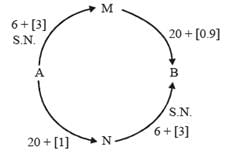
Directions for Questions: Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes).On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.

(2017)

Q. How many cars would be asked to take the route A-N-B, that is Akala-Nanur-Bakala route, by the police department?

Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 1

As there are four cars and as the time through each route is nearly the same, two cars should go through A–M–B and the other two through A–N–B. In case three cars are directed to go through any of the routes, one of the three cars can break the police order and reduce its travel time.

Test: Analytical Reasoning - 1(July 11) - Question 2
Save

Directions for Questions: Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes).On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.

(2017)

Q. If all the car s follow the police order, what is the differen ce in travel time (in minutes) between a car which takes the route A-N-B and a car that takes the route A-M-B?

Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 2


According to the police order 2 cars each would pass through A–M–B and A–N–B.
Then time taken through A–M–B = 29.9 and time taken through A–N–8 = 30.0
∴ Difference = 0.1

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Analytical Reasoning - 1(July 11) - Question 3
Save

Directions for Questions: Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes).On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.

(2017)

Q. A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and AM-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute.
Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
How many cars would the police department order to take the A-M-N-B route so that it is not possible for any car to reduce its travel time by not following the order while the other cars follow the order? (Assume that the police department would never order all the cars to take the same route.)

Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 3

Original time (A–N–B) = 21 + 12 = 33 (three cars) New time = 12 + 20.9 = 32.9
If one car is directed through M–N, one of the car directed through M–B can break the Police order and go through M–N and save time as shown– original time (A–M–B) = 12 (3 cars) + 20.9 = 32.9
New time (A–M–N–B) = 12 + 8 + 12 = 32 Minutes
∴ Only two cars must be directed through M–N Such that any car breaking the Police order can not reduce the travel time.

Test: Analytical Reasoning - 1(July 11) - Question 4
Save

Directions for Questions: Four cars need to travel from Akala (A) to Bakala (B). Two routes are available, one via Mamur (M) and the other via Nanur (N). The roads from A to M, and from N to B, are both short and narrow. In each case, one car takes 6 minutes to cover the distance, and each additional car increases the travel time per car by 3 minutes because of congestion. (For example, if only two cars drive from A to M, each car takes 9 minutes).On the road from A to N, one car takes 20 minutes, and each additional car increases the travel time per car by 1 minute. On the road from M to B, one car takes 20 minutes, and each additional car increases the travel time per car by 0.9 minute.
The police department orders each car to take a particular route in such a manner that it is not possible for any car to reduce its travel time by not following the order, while the other cars are following the order.

(2017)

Q. A new one-way road is built from M to N. Each car now has three possible routes to travel from A to B: A-M-B, A-N-B and AM-N-B. On the road from M to N, one car takes 7 minutes and each additional car increases the travel time per car by 1 minute.
Assume that any car taking the A-M-N-B route travels the A-M portion at the same time as other cars taking the A-M-B route, and the N-B portion at the same time as other cars taking the A-N-B route.
If all the cars follow the police order, what is the minimum travel time (in minutes) from A to B? (Assume that the police department would never order all the cars to take the same route.)
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 4

When all cars follow the Police order the time taken would be A–M–B (1 car)
= 12 + 20 = 32 minutes.
A–M–N–B (2 cars) = 12 + 8 + 12
= 32 minutes.
A–N–B (1 car) = 20 + 12
= 32 minutes.

Test: Analytical Reasoning - 1(July 11) - Question 5
Save

Directions for Questions: A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following.
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day.

(2017)

Q. If the underlying principle is to satisfied in such a way that the journey between any two cities can be performed using only direct (non-stop) flights, then the minimum number of direct flights to be scheduled is.
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 5

Number of ways of selecting two cities from ten cities -10C2
= 10 x 9 / 2
Hence the minimum no. of flights that must be scheduled = 45 × 4 = 180

Test: Analytical Reasoning - 1(July 11) - Question 6
Save

Directions for Questions: A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following.
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day.

(2017)

Q. Suppose three of the ten cities are to be developed as hubs. A hub is a city which is connected with every other city by direct flights each way, both in the morning as well as in the evening. The only direct flights which will be scheduled are originating and /or terminating in one of  the hubs. Then the minimum number of direct flights that need to be scheduled so that the underlying principle of the airline to serve all the ten cities is met without visiting more than one hub during one trip is.
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 6

Let the ten cities be represented by A through J.
Among these ten cities, consider A, B and C to be hubs and the other seven cities to be non-hub cities.
It is given that any direct flight should originate and terminate at a hub.
Total flight from D = 4 × 3 = 12
[∵ Only for A, B, C]
Non hub city flight = 12 × 7 = 84
[∵ for other then A, B, C]
Total flight = 12 + 84 = 96

Test: Analytical Reasoning - 1(July 11) - Question 7
Save

Directions for Questions: A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following.
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day.

(2017)

Q. Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4, having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further, suppose that direct flights are allowed only between two cities satisfying one of the following.
(I) Both cities are in G1
(II) Between A and any city in G2
(III) Between B and any city in G3
(IV) Between C and any city in G4
Then the minimum number of direct flights that satisfies the underlying principle of the airline is.
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 7

Given that G1 has the cities A, B and C. G2, G3 and G4 have 3, 2 and 2 cities respectively. From the given conditions, we can see that a city in G2 cannot be connected by a direct flight to a city in G3 or G4. Hence, for a person to travel from a city in G2 to a city in G3 or G4, all the citres in G2 must be connected to A and from A, he can travel to B or C to travel to a city G3 or G4 respectively.
Hence, the 3 cities in G2 must be connected to A between each pair of cities there must be four flights.
Hence, there must be 4 × 3 = 12 flights between cities in G2 and A.
Since there are 2 cities in G3, there must be 2 × 4 = 8 flights between cities in G3 and 8.
Since there are 2 cities in G4, there must be 2× 4 = 8 flights between cities in G4 and C.
Also, the cities in G1, i.e.,  A, B and C must be connected to each other Hence, there must be an additional 4 × 3 = 12 flights between these three cities.
Therefore, the total minimum number of direct flights that must be scheduled =12 + 8 + 8 + 12 = 40

Test: Analytical Reasoning - 1(July 11) - Question 8
Save

Directions for Questions: A new airlines company is planning to start operations in a country. The company has identified ten different cities which they plan to connect through their network to start with. The flight duration between any pair of cities will be less than one hour. To start operations, the company has to decide on a daily schedule.
The underlying principle that they are working on is the following.
Any person staying in any of these 10 cities should be able to make a trip to any other city in the morning and should be able to return by the evening of the same day.

(2017)

Q. Suppose the 10 cities are divided into 4 distinct groups G1, G2, G3, G4 having 3, 3, 2 and 2 cities respectively and that G1 consists of cities named A, B and C. Further suppose that direct flights are allowed only between two cities satisfying one of the following.
(A) Both cities are in G1
(B) Between a and any city in G2
(C) Between b and any city in G3
(D) Between c and any city in G4
However, due to operational difficulties at A, it was later decided that the only flights that would operate at A would be those to and from B. Cities in G2 would have to be assigned to G3 or G4.
What would be the maximum reduction in the number of direct flights as compared to the situation before the operational difficulties arose?
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 8

It is given that the cities in G2 will be assigned to G3 or G4. However, this, by itself, will not result in any reduction in the number of flights because the cities in G2 will still have to be connected to either 8 or C.
However, it is also given that there are now flights between A and C. Hence, the 4 flights that would have been scheduled in the previous case, will now not be scheduled. Hence, the reduction in the number of flights can be a maximum of 4.

Test: Analytical Reasoning - 1(July 11) - Question 9
Save

Directions for Questions: answer the questions on the basis of the information given below.
A team must be selected from ten probable – A, B, C, D, E, F, G, H, I and J. Of these, A, C, E and are forwards, B, G and H are point guards and D, F and I are defenders.
Further, the following conditions need to be observed:
(i) The team must have at least one forward, one point guard and one defender.
(ii) If the team includes J, it must also include F.
(iii) The team must include E or B, but not both.
(iv) If the team includes G, it must also include F.
(v) The team must include exactly one among C, G and I.
(vi) C and F cannot be members of the same team
(vii) D and H cannot be members of the same team
(viii) The team must include both A and D or neither of them.
There is no restriction on the number of members in the team.

(2016)

Q. What could be the size of the team that includes G?
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 9

The conditions related to G are, if G is included, F also must be included and C and I cannot be included. There are no other conditions related to G. Hence, a team that includes G can be
(a) AEJGDF
(b) ADGFE
(c) EGFH
More arrangement are possible. Hence, the number of members in the team is 4 or 5.

Test: Analytical Reasoning - 1(July 11) - Question 10
Save

Directions for Questions: answer the questions on the basis of the information given below.
A team must be selected from ten probable – A, B, C, D, E, F, G, H, I and J. Of these, A, C, E and are forwards, B, G and H are point guards and D, F and I are defenders.
Further, the following conditions need to be observed:
(i) The team must have at least one forward, one point guard and one defender.
(ii) If the team includes J, it must also include F.
(iii) The team must include E or B, but not both.
(iv) If the team includes G, it must also include F.
(v) The team must include exactly one among C, G and I.
(vi) C and F cannot be members of the same team
(vii) D and H cannot be members of the same team
(viii) The team must include both A and D or neither of them
There is no restriction on the number of members in the team.

(2016)

Q. What would be the size of the largest possible team?
Detailed Solution for Test: Analytical Reasoning - 1(July 11) - Question 10

The largest possible team can have six members. As one of, (E, B) and (D, H) and two of (C, G, I) must definitely be excluded. Hence, a miniumum of four members must be excluded. So size of the largest possible team is 6.

152 docs|327 tests
Join Course
Information about Test: Analytical Reasoning - 1(July 11) Page
In this test you can find the Exam questions for Test: Analytical Reasoning - 1(July 11) solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Analytical Reasoning - 1(July 11), EduRev gives you an ample number of Online tests for practice

Top Courses for CAT

Download as PDF

Top Courses for CAT

Important Questions for Analytical Reasoning - 1(July 11)

Find all the important questions for Analytical Reasoning - 1(July 11) at EduRev.Get fully prepared for Analytical Reasoning - 1(July 11) with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Analytical Reasoning - 1(July 11) syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Analytical Reasoning - 1(July 11) resources.

Analytical Reasoning - 1(July 11) MCQs with Answers

Prepare for the Analytical Reasoning - 1(July 11) within the CAT exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Analytical Reasoning - 1(July 11) Daily Test for CAT Preparation

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Analytical Reasoning - 1(July 11) with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup