Test: Areas Of Parallelograms And Triangles- 1 - Class 9 MCQ
25 Questions MCQ Test - Test: Areas Of Parallelograms And Triangles- 1
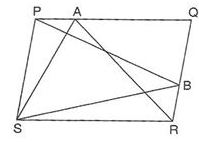
PQRS is a parallelogram and A and B are any points on PQ and QR. If ar(║;PQRS) = 48cm2, then ar(△PBS) +ar(△ASR) is equal to
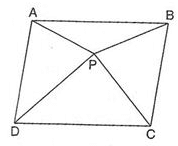
In the given figure ABCD is a parallelogram and its area is 64cm2. If P is any point in the interior of ║ABCD, then ar (△APD) +ar(△PBC) is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
ABCD is a parallelogram. O is any point on diagonal BD. If ar(△DOP) = 8cm2, ar(△BOS) = 3cm2 and ar(△APS) = 6cm2,then ar(║ABCD) is
ABC is a triangle in which D is the mid-point of BC. E and F are mid-points of DC and AE respectively. If ar(△ABC)=16cm2, then ar(△DEF) is
The median of a triangle divides it into two
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar(PQRS) = 36cm2, then ar (ABCD) is
PQRS is a trapezium with PQ║SR. A line parallel to PR intersects PQ at X and QR at Y. If ar(△PYR) = 5cm2,then ar(△PXS) is
In the given figure, ABCD is a rectangle and EFGH is a trapezium DE = CH. If ar(ABCD)=26cm2, then ar (EFGH) is
If AD is median of △ABC and P is a point on AC such that ar(△ADP):ar(△ABD) = 2:3, then ar(△PDC) : ar(△ABC) is
ABCD is quadrilateral whose diagonal AC divides it into two parts, equal in area, then ABCD
ABCD is a trapezium in which AB║DC.If ar(△ABD) = 24cm2and AB = 8 cm, then the height of △ABC is
D and E are mid-points of BC and AD respectively. If ar(△ABC) = 10cm2, then ar(△EBC)ar is
ABCD, ABEF and AGHF are parallelograms. If ar(ABCD) = 23cm2, then ar (FGH) is
The altitude of a parallelogram is twice the length of the base and its area is 1250cm2. The lengths of the base and the altitude respectively are :
Two parallelograms are on equal bases and between the same parallels. The ratio of their areas is
In the given figure if ar(║ABCD)=29cm2 and AB = 5.8 cm, then the height of ║ABEF is
Points A, B, C, and D are collinear. AB = BC = CD. XY║AD. If P and M lie on XY and ar(△MCD) = 7cm2,then ar(△APB) and ar(△APD) respectively are
ABCD is a parallelogram in which DC is produced to P such that DC = CP. AP intersects BC at Q. If ar(△BQD) = 3cm2,then ar(║ABCD) is
ABCD is a parallelogram one of whose diagonals is AC. Then, which of the following is true?
If a triangle and a parallelogram are on the same base and between the same parallels, then the ratio of the area of the triangle to the area of the parallelogram is
AP ║ BQ ║ CR. If ar(△AQC)=17cm2, then ar(△PBR)ar(△PBR) is
If E and F are mid-points of sides AB and CD respectively and ar(║ABCD)=36cm2,thenar(APD):ar(DEF)
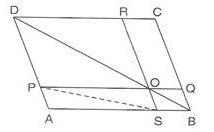
PQRS is a parallelogram whose diagonals PR and SQ intersect at O. A line segment through O meets PQ at A and SR at B. If ar(PQRS) = 25cm2, then ar (SBAP) is
In the figure, ABCD is a parallelogram and EFCD is rectangle. Now which of the following is correct option ?
Diagonals AC and BD of trapezium ABCD in which AB ║ DC, intersect each other at O. The triangle which is equal in area to triangle AOD is

















