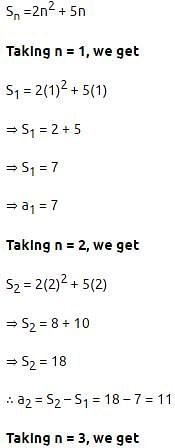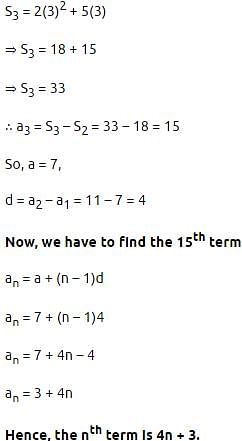Test: Arithmetic And Geometric Progressions - 3 - CA Foundation MCQ
30 Questions MCQ Test Quantitative Aptitude for CA Foundation - Test: Arithmetic And Geometric Progressions - 3
In an A.P., if common difference is 2, Sum of n terms is 49, 7th term is 13 tthen then n = _________.
If 8th term of an A.P. is 15, then sum of its 15 terms is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the sum of n terms of an A.P. be 2n2 + 5n, then its 'nth' term is
If 'n' arithmetic means are inserted between 7 & 71 and 5th arithmetic mean is 27, then 'n' is equal to:
If the sum of n terms of an A.P. be 3n2 - n and its common difference is 6, then its first terms is:
In a G.P. the sixth term is 729 and the common difference is 3, then the first term is G.P. is:
The 4th term of an A.P. is three times the first and the 7th term excessds twice the third term by 1. Find the first term 'a' and common difference 'd'.
The first term of a G.P. where second term is 2 and sum of infinite term is 8 will be
If the sum of the 4th term and the 12th term of an A.P. is 8, what is the sum of the first 15 terms of the progression?
An Arithmetic progression has 13 terms whose sum is 143. The third term is 5 so the first term si
If a1, a2, a3 represents first, second and third terms of an AP respectively, the first terms is 2 and (a1 + a2)a3 is minimum, then the common difference is equal to
If each month Rs.100 increase in any sum then find out the total sum after 10 months, if the sum of first month is Rs.2,000.
The sum of all two Digit odd numbers is
Insert two Arithmetic means between 68 and 260
The sum of third and ninth term of an A.P is 8. Find the sum of the first 11 terms of the progression.
Find the product of:
(243), (243)1/6 , (243)1/36,.........∞
If sum of 3 arithmetic means between "a" and 22 us 42, then "a" =____
The numbers x, 8, y are in G.P. and the numbers x, y, -8 are in A.P. The values of x, y are _________.
Divide 144 into three parts which are in AP and such that the largest is twice and smallest, the smallest of three numbers will be:
If Sum (Sn) of 'n'-terms of an Arithmetic Progression is (2n2+n).What is the difference of its 10th and 1st terms?
Find the number whose arithmetic mean is 12.5 and geometric mean is 10.
If the sum of infinite terms in a G.P. is 2 and the sum of their squares is 4/3 the series is
The sum upto infinity of the series 2/3+5/9+2/27+5/81+…..is
Three numbers in G.P. with their sum 13/3 and sum of their squares 91/9 are _______.
Three numbers in G.P. with their sum 130 and their product 27000 are _________.
If the continued product of three numbers in G.P. is 27 and the sum of their products in pairs is 39 the numbers are_______.
The sum upto infinity of the series 4+0.8+0.16+…….is
Find five numbers in G.P. such that their product is 32 and the product of the last two is 108.
The sum upto infinity of the series 1/2+1/6+1/18+……is
The sum upto infinity of the series 4/7-5/72+4/73-5/74+……..is
|
114 videos|164 docs|98 tests
|
|
114 videos|164 docs|98 tests
|