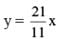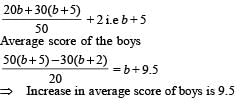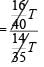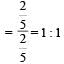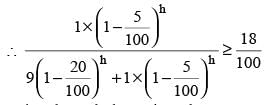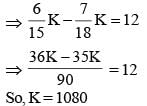Test: Average, Ratio & Proportion - CAT MCQ
20 Questions MCQ Test Topic-wise Past Year Questions for CAT - Test: Average, Ratio & Proportion
The salaries of Ramesh, Ganesh and Rajesh were in the ratio 6:5:7 in 2010, and in the ratio 3:4:3 in 2015. If Ramesh’s salary increased by 25% during 2010-2015, then the percentage increase in Rajesh’s salary during this period is closest to
(2019)
The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
(2019)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In an examination, Rama’s score was one-twelfth of the sum of the scores of Mohan and Anjali. After a review, the score of each of them increased by 6. The revised scores of Anjali, Mohan, and Rama were in the ratio 11 : 10 : 3. Then Anjali’s score exceeded Rama’s score by
(2019)
The strength of a salt solution is p% if 100 ml of the solution contains p grams of salt. Each of three vessels A, B, C contains 500 ml of salt solution of strengths 10%, 22%, and 32%, respectively. Now, 100 ml of the solution in vessel A is transferred to vessel B. Then, 100 ml of the solution in vessel B is transferred to vessel C. Finally, 100 ml of the solution in vessel C is transferred to vessel A. The strength, in percentage, of the resulting solution in vessel A is
(2019)
A chemist mixes two liquids 1 and 2. One litre of liquid 1 weighs 1 kg and one litre of liquid 2 weighs 800 gm. If half litre of the mixture weighs 480 gm, then the percentage of liquid 1 in the mixture, in terms of volume, is
(2019)
Amala, Bina, and Gouri invest money in the ratio 3 : 4 : 5 in fixed deposits having respective annual interest rates in the ratio 6 : 5 : 4. What is their total interest income (in Rs) after a year, if Bina’s interest income exceeds Amala’s by ₹ 250?
(2019)
Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is
(2019)
Corners are cut off from an equilateral triangle T to produce a regular hexagon H. Then, the ratio of the area of H to the area of T is
(2019)
A CAT aspirant appears for a certain number of tests. His average score increases by 1 if the first 10 tests are not considered, and decreases by 1 if the last 10 tests are not considered. If his average scores for the first 10 and the last 10 tests are 20 and 30, respectively, then the total number of tests taken by him is
(2018)
In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?
(2018)
Two types of tea, A and B, are mixed and then sold at Rs. 40 per kg. The profit is 10% if A and B are mixed in the ratio 3 : 2, and 5% if this ratio is 2 : 3. The cost prices, per kg, of A and B are in the ratio.
(2018)
Raju and Lalitha originally had marbles in the ratio 4:9. Then Lalitha gave some of her marbles to Raju. As a result, the ratio of the number of marbles with Raju to that with Lalitha became 5:6. What fraction of her original number of marbles was given by Lalitha to Raju?
(2018)
A class consists of 20 boys and 30 girls. In the mid-semester examination, the average score of the girls was 5 higher than that of the boys. In the final exam, however, the average score of the girls dropped by 3 while the average score of the entire class increased by 2. The increase in the average score of the boys is
(2017)
A stall sells popcorn and chips in packets of three sizes : large, super, and jumbo. The numbers of large, super, and jumbo packets in its stock are in the ratio 7 : 17 : 16 for popcorn and 6 : 15 : 14 for chips. If the total number of popcorn packets in its stock is the same as that of chips packets, then the numbers of jumbo popcorn packets and jumbo chips packets are in the ratio
(2017)
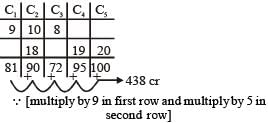
Suppose, C1, C2, C3, C4 and C5 are five companies. The profits made by C1, C2 and C3 are in the ratio 9 : 10 : 8 while the profits made by C2, C4, and C5 are in the ratio 18 : 19 : 20. If C5 has made a profit of ₹19 crore more than C1, then the total profit (in ₹) made by all five companies is
(2017)
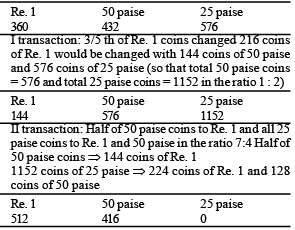
A certain sum of money is made up of Re. 1, 50 paise and 25 paise coins. The ratio of the number of these coins is 5 : 6 : 8. Then, 3/5th of the Re. 1 coins are changed to 50 paise and 25 paise coins, such that the ratio of the total number of these coins in the same order became 1 : 2. Now, half of the 50 paise coins are changed to Re. 1 coins and all the 25 paise coins are changed to Re.1 and 50 paise coins in the ratio 7 : 4. What is the ratio of the Re. 1 and 50 paise coins at the end of the conversions?
(Note: If you change a Re.1 coin into 50 paise coins, then you will get two coins of 50 paise for a Re. 1 coin.)
(2015)
There are 40 students in a class. A student is allowed to shake hand only once with a student who is taller than him or equal in height to him. He can’t shake hand with anyone who is shorter than him. Average height of the class is 5 feet. What is the difference between the maximum and minimum number of handshakes that can take place in the class?
(2015)
The ratio of alcohol to water in an alcohol-water solution is 9 : 1. The rate of evaporation per hour of alcohol and water on boiling is 20% and 5% respectively. The minimum number of hours for which the solution needs to be boiled so as it contains at least 18% of water?
(2013)
Three men are gambling in Casino Royal. They start with sums of money in the ratio 7 : 6 : 5 and finish with sums of money in the ratio 6 : 5 : 4, in the same order as before. One of them won $ 12. How many dollars did he start with ? [The three men gambled amongst each other only]
(2012)
The letters of the English alphabet, in the order A to Z, are made to represent 26 numbers which are in Arithmetic Progression. The sum of the numbers representing A, C and E is 36 while that of A, C, E and G is 60. What is the sum of the numbers representing B, D, F and H?
(2011)
|
43 docs|31 tests
|
|
43 docs|31 tests
|


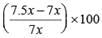 ≈ 7
≈ 7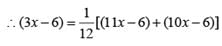
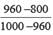 = 4 / 1
= 4 / 1

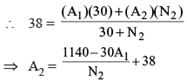
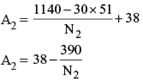
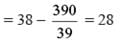
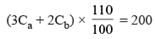
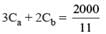
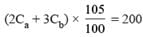
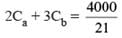
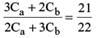
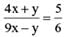 ⇒
⇒