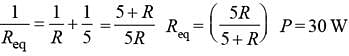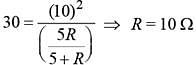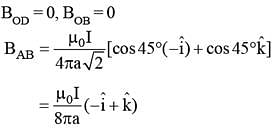Test: BITSAT Past Year Paper- 2010 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2010
If P represents radiation pressure, c represents speed of light and Q represents radiation energy striking a unit area per second, the non-zero integers x, y and z such that PxQycz is dimensionless, are.
The position x of a particle varies with time (t) as x = A t2 – B t3. The acceleration at time t of the particle will be equal to zero. What is the value of t?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two projectiles A and B are thrown with the same speed but angles are 40º and 50º with the horizontal. Then
A body is travelling in a circle at a constant speed. It
Two blocks are connected over a massless pulley as shown in fig. The mass of block A is 10 kg and the coefficient of kinetic friction is 0.2. Block A slides down the incline at constant speed. The mass of block B in kg is:

A spring is compressed between two toy carts of mass m1 and m2. When the toy carts are released, the springs exert equal and opposite average forces for the same time on each toy cart. If v1 and v2 are the velocities of the toy carts and there is no friction between the toy carts and the ground, then :
The potential energy for a force field 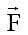 is given by U (x, y) = cos (x + y). The force acting on a particle at position given by coordinates (0, π/4) is –
is given by U (x, y) = cos (x + y). The force acting on a particle at position given by coordinates (0, π/4) is –
A long string is stretched by 2 cm and the potential energy is V. If the spring is stretched by 10 cm, its potential energy will be
The ratio of the accelerations for a solid sphere (mass ‘m’ and radius ‘R’) rolling down an incline of angle ‘θ’ without slipping and slipping down the incline without rolling is:
A system consists of three particles, each of mass m and located at (1, 1), (2, 2) and (3, 3). The co-ordinates of the centre of mass are
Suppose the gravitational force varies inversely as the nth power of distance. Then the time period of a planet in circular orbit of radius ‘R’ around the sun will be proportional to
Two planets A and B have the same material density. If the radius of A is twice that of B, then the ratio of the escape velocity vA/vB is
The upper end of a wire of diameter 12mm and length 1m is clamped and its other end is twisted through an angle of 30°. The angle of shear is
A spherical ball is dropped in a long column of a viscous liquid. The speed (v) of the ball as a function of time (t) may be best represented by
Two mercury drops (each of radius r) merge to form a bigger drop. The surface energy of the bigger drop, if T is the surface tension, is
Two circular plates of radius 5 cm each, have a 0.01 mm thick water film between them. Then what will be the force required to separate these plate (S.T. of water = 73 dyne/cm) ?
One kilogram of ice at 0°C is mixed with one kilogram of water at 80°C. The final temperature of the mixture is (Take specific heat of water = 4200 kJ/kg-°C, Latent heat of ice = 336 kJ/kg)
In the equation PVγ = constant, the value of γ is unity. Then the process is
An ideal refrigerator has a freezer at a temperature of 13ºC. The coefficient of performance of the engine is 5. The temperature of the air (to which heat is rejected) is
3 moles of an ideal gas at a temperature of 27°C are mixed with 2 moles of an ideal gas at a temperature 227°C, determine the equilibrium temperature of the mixture, assuming no loss of energy.
A simple pendulum has time period 't'. Its time period in a lift which is moving upwards with acceleration 3 ms–2 is
A wave y = a sin (ωt – kx) on a string meets with another wave producing a node at x = 0. Then the equation of the unknown wave is
A source of sound produces waves of wavelength 60 cm when it is stationary. If the speed of sound in air is 320 m s-1 and source moves with speed 20 m s-1, the wavelength of sound in the forward direction will be nearest to
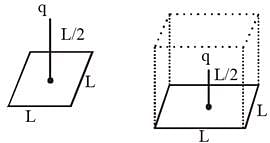
A charge +q is at a distance L/2 above a square of side L. Then what is the flux linked with the surface?
Two metallic spheres of radii 1 cm and 3 cm are given charges of -1 × 10-2 C and 5 × 10-2 C, respectively. If these are connected by a conducting wire, the final charge on the bigger sphere is
In a region, the potential is represented by V(x, y, z) = 6x - 8xy - 8y + 6yz, where V is in volts and x, y, z are in metres. The electric force experienced by a charge of 2 coulomb situated at point (1, 1, 1) is :
The power dissipated in the circuit shown in the figure is 30 Watts. The value of R is
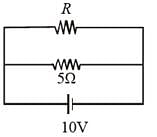
Which of the following quantities do not change when a resistor connected to a battery is heated due to the current?
The magnetic field at the origin due to the current flowing in the wire is –

The back emf induced in a coil, when current changes from 1 ampere to zero in one milli-second, is 4 volts, the self inductance of the coil is


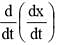 = 2 A - 6Bt
= 2 A - 6Bt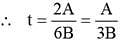
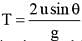 lesser is the value of θ, lesser is sinq and hence lesser will be the time taken. Hence A will fall earlier.
lesser is the value of θ, lesser is sinq and hence lesser will be the time taken. Hence A will fall earlier.
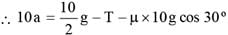
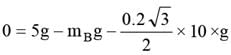
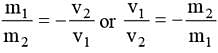
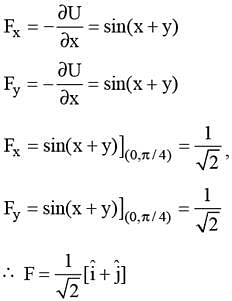

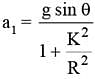
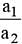
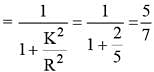
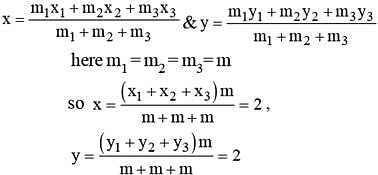

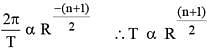

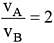
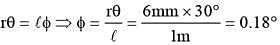
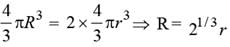
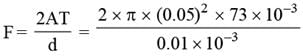
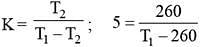
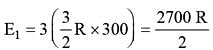
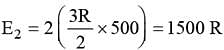
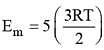
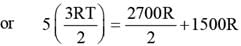
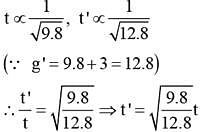
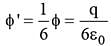
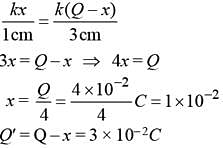
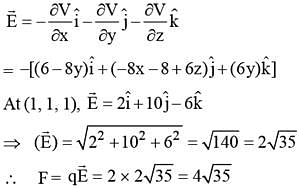
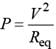 ...(i)
...(i)