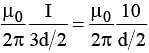Test: BITSAT Past Year Paper- 2013 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2013
The velocity and acceleration vectors of a particle undergoing circular motion are 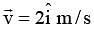 and
and 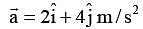 respectively at an in stant of time. The radius of the circle is –
respectively at an in stant of time. The radius of the circle is –
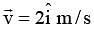 and
and 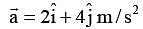 respectively at an in stant of time. The radius of the circle is –
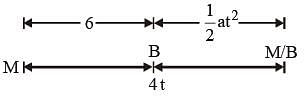
respectively at an in stant of time. The radius of the circle is –A man runs at a speed of 4 m/s to overtake a standing bus. When he is 6 m behind the door at t = 0, the bus moves forward and continuous with a constant acceleration of 1.2 m/s2. The man reaches the door in time t. Then,
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Wave pulse can travel along a tense string like a violin spring. A series of experiments showed that the wave velocity V of a pulse depends on the following quantities, the tension T of the string, the cross-section area A of the string and then as per unit volume ρ of the string. Obtain an expression for V in terms of the T, A and r using dimensional analysis.
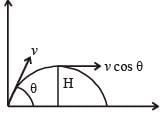
A body is projected, making an acute angle with the horizontal. If angle between velocity 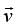 and acceleration
and acceleration 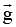 is θ, then
is θ, then
The minimum velocity (in ms–1) with which a car driver must traverse a flat curve of radius 150 m and coefficient of friction 0.6 to avoid skidding is
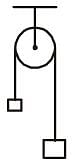
A bob is hanging over a pulley inside a car through, a string. The second end of the string is in the hand of a person standing in the car. The car is moving with constant acceleration 'a' directed horizontally as shown in figure. Other end of the string is pulled with constant acceleration ‘a’ vertically. The tension in the string is equal to –
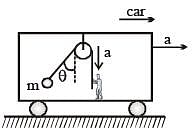
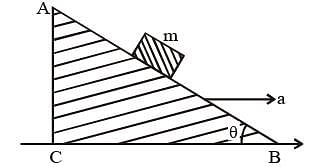
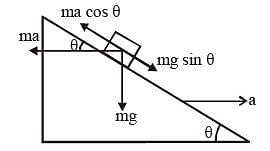
A block of mass m is placed on a smooth inclined wedge ABC of inclination q as shown in the figure. The wedge is given an acceleration ‘a’ towards the right. The relation between a and θ for the block to remain stationary on the wedge is
A 3.628 kg freight car moving along a horizontal rail road spur track at 7.2 km/hour strikes a bumper whose coil springs experiences a maximum compression of 30 cm in stopping the car. The elastic potential energy of the springs at the instant when they are compressed 15 cm is
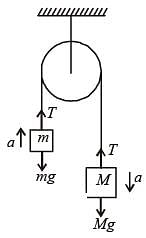
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.
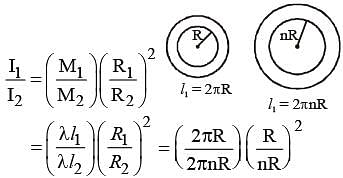
Two rings of radius R and nR made of same material have the ratio of moment of inertia about an axis passing through centre is 1 : 8. The value of n is
A particle of mass ‘m’ is projected with a velocity v making an angle of 30° with the horizontal. The magnitude of angular momentum of the projectile about the point of projection when the particle is at its maximum height ‘h’ is
There is a shell of mass M and density of the shell is uniform. The work done to take a point mass from point A to B is [AB = r]

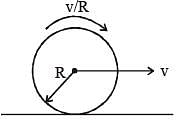
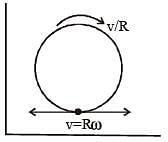
A disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in figure. At any instant, for the lower most point of the disc –
A cube is subjected to a uniform volume compression. If the side of the cube decreases by 2% the bulk strain is
A ball whose density is 0.4 × 103 kg/m3 falls into water from a height of 9 cm. To what depth does the ball sink ?
Figure shows a copper rod joined to a steel rod.
The rods have equal length and equal crosssectional area. The free end of the copper rod is kept at 0ºC and that of steel rod is kept at 100ºC.
Find the temperature of the junction of the rod.
Conductivity of copper = 390 W/mºC.
Conductivity of steel = 46 W/m ºC

If the radius of a star is R and it acts as a black body, what would be the temperature of the star, in which the rate of energy production is Q ?
A thermodynamical system is changed from state (P1, V1) to (P2, V2) by two different process, the quantity which will remain same will be
A Car not’s heat engine works between the temperatures 427°C and 27°C. What amount of heat should it consume per second to deliver mechanical work at the rate of 1.0 kW?
A vessel containing 1 more of O2 gas (molar mass 32) at temperature T. The pressure of the gas is p.An identical vessel containing one mole of he gas (molar mass 4) at temperature 2T has a pressure of
The temperature of an ideal gas is increased from 27°C to 127°C, then percentage increase in vrms is
Two gases occupy two containers A and B the gas in A, of volume 0.10m3, exerts a pressure of 1.40 MPa and that in B of volume 0.15m3 exerts a pressure 0.7 MPa. The two containers are united by a tube of negligible volume and the gases are allowed to intermingle. Then if the temperature remains constant, the final pressure in the container will be (in MPa)
An instan tan eous displacemen t of a simple harmonic oscillator is x = A cos (ωt + p/4). Its speed will be maximum at time
Two waves of wavelengths 99 cm and 100 cm both travelling with velocity 396 m/s are made to interfere. The number of beats produced by them per second is
If equation of transverse wave is y = x0 cos 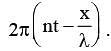 Maximum velocity of particle istwice of wave velocity, if l is
Maximum velocity of particle istwice of wave velocity, if l is
Three equal charges (q) are placed at corners of an equilateral triangle of side a. The force on any charge is
Two identical capacitors, have the same capacitance C. One of them is charged to potential V1 and the other to V2. The negative ends of the capacitors are connected together. When the positive ends are also connected, the decrease in energy of the combined system is –
What should be the characteristic of fuse wire?
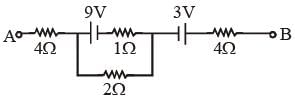
In the circuit shown in figure potential difference between points A and B is 16 V. the current passing through 2Ω resistance will be
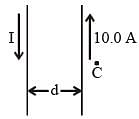
Two parallel conductors carry current in opposite directions as shown in figure. One conductor carries a current of 10.0 A. Point C is a distance d/2 to the right of the 10.0 A current. If d = 18 cmand I is adjusted so that the magnetic field at C is zero, the value of the current I is


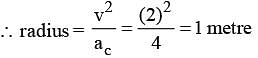
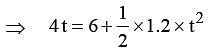
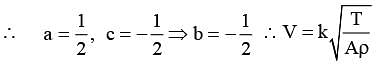
 and ar is more than 0º and
and ar is more than 0º and  less than 180º.
less than 180º.

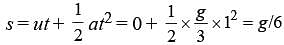

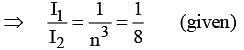

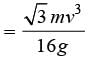
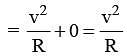
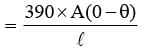
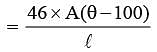
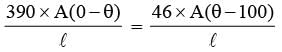
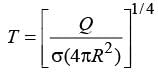
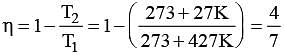
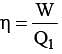
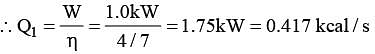
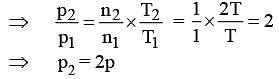
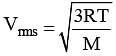
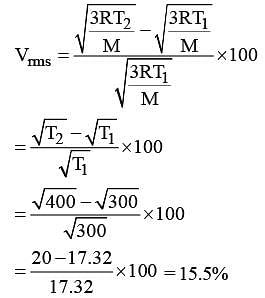
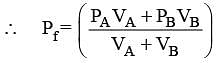
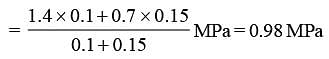
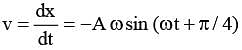
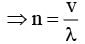
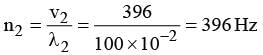
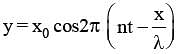
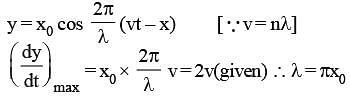
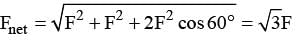
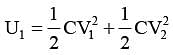
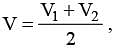
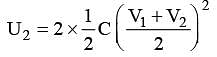

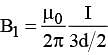 (since, point C is separated by
(since, point C is separated by 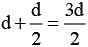 from 1st conductor). The direction of field is perpendicular to the plane of paper and directed outwards.
from 1st conductor). The direction of field is perpendicular to the plane of paper and directed outwards.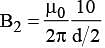 (since, point C is separated by d/2 from 2nd conductor)
(since, point C is separated by d/2 from 2nd conductor)