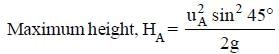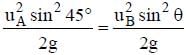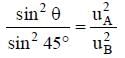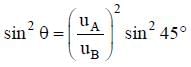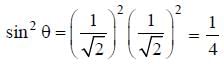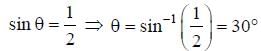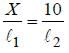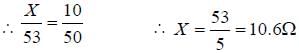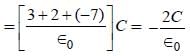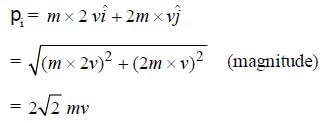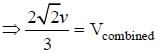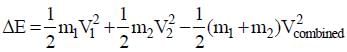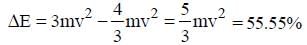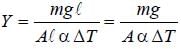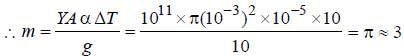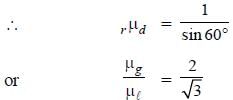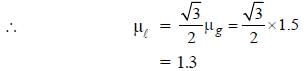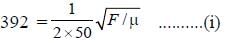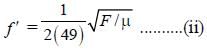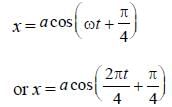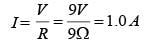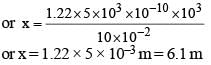Test: BITSAT Past Year Paper- 2017 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2017
What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
A mercury drop of radius 1 cm is sprayed into 106 drops of equal size. The energy expressed in joule is (surface tension of Mercury is 460 × 10–3 N/m)
Two plano-concave lenses (1 and 2) of glass of refractive index 1.5 have radii of curvature 25 cm and 20 cm. They are placed in contact with their curved surface towards each other and the space between them is filled with liquid of refractive index 4/3. Then the combination is
A charged particle moves through a magnetic field perpendicular to its direction. Then
After two hours, one-sixteenth of the star ting amount of a certain radioactive isotope remained undecayed. The half life of the isotope is
A coil of inductance 300 mH and resistance 2Ω is connected to a source of voltage 2 V. The current reaches half of its steady state value in
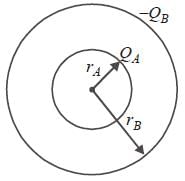
Two concentric conducting thin spherical shells A, and B having radii rA and rB ((rB > rA) are charged to QA and –QB (|QB| > |QA|). The electric field along a line passing through the centre is
A capillary tube of radius R is immersed in water and water rises in it to a height H. Mass of water in the capillary tube is M. If the radius of the tube is doubled, mass of water that will rise in the capillary tube will now be :
A sonometer wire resonates with a given tuning fork forming standing waves with five antinodes between the two bridges when a mass of 9 kg is suspended from the wire. When this mass is replaced by a mass M, the wire resonates with the same tuning fork forming three antinodes for the same positions of the bridges. The value of M is
When a metal surface is illuminated by light of wavelengths 400 nm and 250 nm, the maximum velocities of the photoelectrons ejected are v and 2v respectively. The work function of the metal is (h - Planck's constant, c = velocity of light in air)
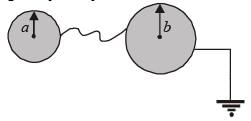
Two conductin g shells of radius a an d b are connected by conducting wire as shown in figure.
The capacity of system is :
When 92U235 under goes fission , 0.1% of its original mass is changed into energy. How much energy is released if 1 kg of 92U235 undergoes fission
One mole of an ideal gas is taken from state A to state B by three different processes,
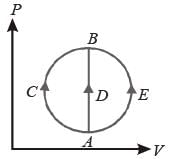
(i) ACB (ii) ADB (iii) AEB as shown in the P-V diagram. The heat absorbed by the gas is
In the formula X = 3 YZ2, X and Z have dimensions of capacitance and magnetic induction respectively. The dimensions of Y in MKSA system are :
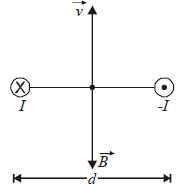
Two very long, straight, parallel wires carry steady currents I and -I respectively. The distance between the wires is d. At a certain instant of time, a point charge q is at a point equidistant from the two wires, in the plane of the wires. Its instantaneous velocity v is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is
Two projectiles A and B thrown with speeds in the ratio 1: √2 acquired the same heights. If A is thrown at an angle of 45° with the horizontal, the angle of projection of B will be
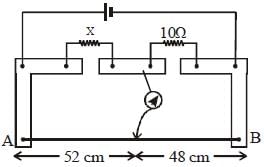
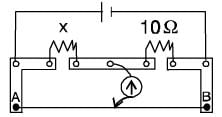
A meter bridge is set up as shown, to determine an unknown resistance ‘X’ using a standard 10 ohm resistor. The galvanometer shows null point when tapping-key is at 52 cm mark. The endcorrections are 1 cm and 2 cm respectively for the ends A and B. The determined value of ‘X’ is
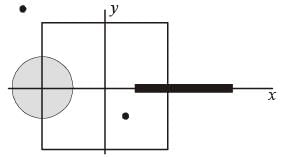
A dis k of r ad ius a/4 having a uniformly distributed charge 6 C is placed in the x - y plane with its centre at (–a / 2, 0, 0). A rod of length a carrying a uniformly distributed charge 8C is placed on the x-axis from x = a /4 to x = 5a / 4.
Two point charges – 7 C and 3 C are placed at (a/4, – a/4, 0) and (– 3a/4, 3a/4, 0), respectively. Consider a cubical surface formed by six surfaces x = ± a/2, y = ± a/2, z = ± a/2. The electric flux through this cubical surface is
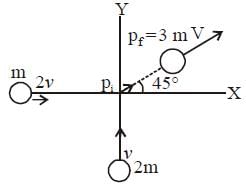
A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
A coil is suspended in a uniform magnetic field, with the plane of the coil parallel to the magnetic lines of force. When a current is passed through the coil it starts oscillating; It is very difficult to stop. But if an aluminium plate is placed near to the coil, it stops. This is due to :
A steel wire of length ‘L’ at 40°C is suspended from the ceiling and then a mass ‘m’ is hung from its free end. The wire is cooled down from 40°C to 30°C to regain its original length ‘L’. The coefficient of linear thermal expansion of the steel is 10–5/°C, Young’s modulus of steel is 1011 N/ m2 and radius of the wire is 1 mm. Assume that L >> diameter of the wire. Then the value of ‘m’ in kg is nearly
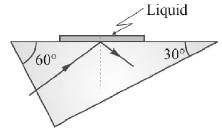
On a hypotenuse of a right prism (30° – 60° – 90°) of refractive index 1.50, a drop of liquid is placed as shown in figure. Light is allowed to fall normally on the short face of the prism. In order that the ray of light may get totally reflected, the maximum value of refractive index is :
A tuning fork of frequency 392 Hz, resonates with 50 cm length of a string under tension (T). If length of the string is decreased by 2%, keeping the tension constant, the number of beats heard when the string and the tuning fork made to vibrate simultaneously is :
Hydrogen (H), deuterium (D), sin gly ionized helium (He+) and doubly ionized lithium (Li++) all have one electron around the nucleus. Consider n = 2 to n = 1 transition. The wavelengths of emitted radiations are λ1, λ2, λ3 and λ4 respectively.Then approximately :
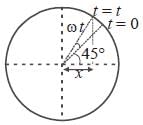
The following figure depict a circular motion. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure.
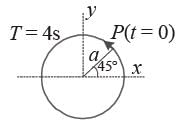
The simple harmonic motion of the x-projection of the radius vector of the rotating particle P can be shown as :
There are two sources kept at distances 2λ. A large screen is perpendicular to line joining the sources. Number of maximas on the screen in this case is (λ = wavelength of light)

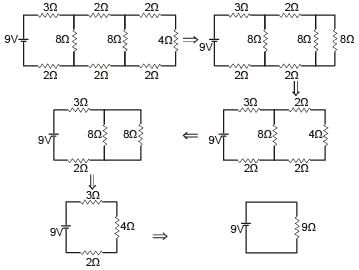
In the circuit shown in figure the current through

A telescope has an objective lens of 10 cm diameter and is situated at a distance of one kilometer from two objects. The minimum distance between these two objects, which can be resolved by the telescope, when the mean wavelength of light is 5000 Å, is of the order of
During vapourisation
I. change of state from liquid to vapour state occurs.
II. temperature remains constant.
III. both liquid and vapour states coexist in equilibrium.
IV. specific heat of substance increases.
Correct statements are
A wire is connected to a battery between the point M and N as shown in the figure (1). The same wire is bent in the form of a square and then connected to the battery between the points M and N as shown in the figure (2). Which of the following quantities increases ?




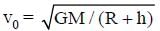
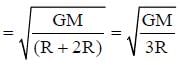
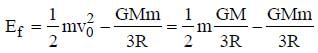
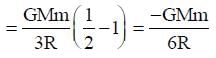
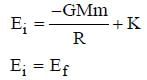
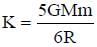

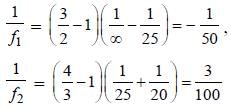

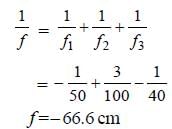
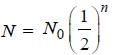
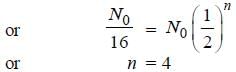

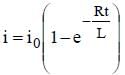

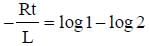
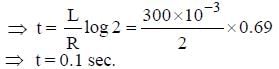
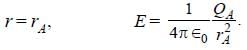

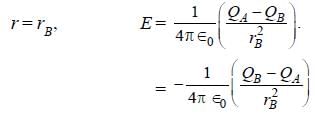
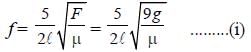
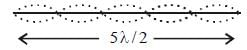
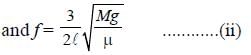
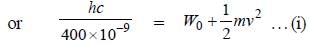
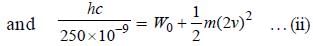
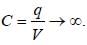
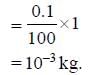
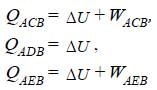
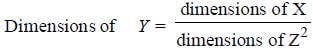
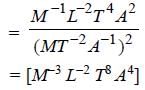
 is 180°,
is 180°,