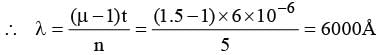Test: BITSAT Past Year Paper- 2020 - JEE MCQ
30 Questions MCQ Test - Test: BITSAT Past Year Paper- 2020
An organ pipe, open from both end produces 5 beats per second when vibrated with a source of frequency 200 Hz. The second harmonic of the same pipes produces 10 beats per second with a source of frequency 420 Hz. The fundamental frequency of organ pipe is
A vessel of depth 2d cm is half filled with a liquid of refractive index μ1 and the upper half with a liquid of refractive index μ2. The apparent depth of the vessel seen perpendicularly is
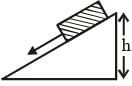
The upper half of an inclined plane with inclination f is perfectly smooth while the lower half is rough.A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
A body of density ρ' is dropped from rest at a height h into a lake of density r where ρ > ρ' neglecting all dissipative forces, calculate the maximum depth to which the body sinks before returning to float on the surface :
If the forward voltage in a semiconductor diode is changed from 0.5V to 0.7 V, then the forward current changes by 1.0 mA. The forward resistance of diode junction will be
The heat generated in a cir cuit is given by Q = I2 Rt, where I is current, R is resistance and t is time. If the percentage errors in measuring I, R and t are 2%, 1% and 1% respectively, then the maximum error in measuring heat will be
The r.m.s. velocity of oxygen molecule at 16ºC is 474 m/sec. The r.m.s. velocity in m/s of hydrogen molecule at 127ºC is
A projectile A is thrown at an angle of 30° to the horizontal from point P. At the same time, another projectile B is thrown with velocity v2 upwards from the point Q vertically below the highest point. For B to collide with A, 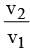 should be
should be

The coefficient of friction between the rubber tyres and the road way is 0.25. The maximum speed with which a car can be driven round a curve of radius 20 m without skidding is (g = 9.8 m/s2)
A boy pushes a toy box 2.0 m along the floor by means of a force of 10 N directed downward at an angle of 60º to the horizontal. The work done by the boy is
The engine of a truck moving along a straight road delivers constant power. The distance travelled by the truck in time t is proportional to
The escape velocity from a planet is ve. A tunnel is dug along a diameter of the planet and a small body is dropped into it at the surface. When the body reaches the centre of the planet, its speed will be
If the the earth is at one-fourth of its present distance from the sun, the duration of year will be
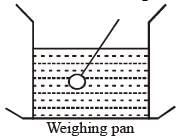
A vessel with water is placed on a weighing pan and it reads 600 g. Now a ball of mass 40 g and density 0.80 g cm–3 is sunk into the water with a pin of negligible volume, as shown in figure keeping it sunk. The weighing pan will show a reading
In an adiabatic process, the pressure is increased by 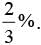 If γ = 3/2, then the volume decreases by
If γ = 3/2, then the volume decreases by
nearly
The equation of a projectile is  The angle of projection is given by
The angle of projection is given by
Two wires A and B of the same material, having radii in the ratio 1 : 2 and carry currents in the ratio 4 : 1. The ratio of drift speed of electrons in A and B is
An instantaneous displacemen t of a simple harmonic oscillator is x = A cos (ωt + π/4). Its speed will be maximum at time
The energy of electron in the n th orbit of hydrogen atom is expressed as 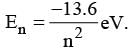
The shortest and longest wavelength of Lyman series will be
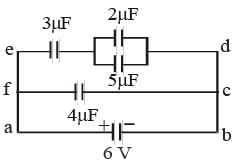
In the circuit given below, the charge in μC, on the capacitor having 5 μF is
A crystal has a coefficient of expansion 13×10– 7 in one direction and 231 × 10–7 in every direction at right angles to it. Then the cubical coefficient of expansion is
A solid cylinder and a hollow cylinder both of the same mass and same external diameter are released from the same height at the same time on an inclined plane. Both roll down without slipping. Which one will reach the bottom first?
A whistle of frequency 1000 Hz is sounded on a car travelling towards a cliff with velocity of 18 m s–1 normal to the cliff. If c = 330 m s–1, then the apparent frequency of the echo as heard by the car driver is nearly
A thin sheet of glass (μ = 1.5) of thickness 6 micron introduced in the path of one of the interfering beams in a double slit experiment shifts the central fringe to a position previously occupied by fifth bright fringe. Then the wavelength of light used is
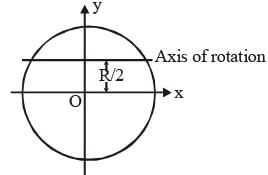
M.I of a circular loop of radius R about the axis in figure is
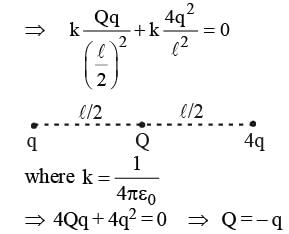
Three charge q, Q and 4q are placed in a straight line of length l at points distant 0, 1/2
and l respectively from one end. In order to make the net froce on q zero, the charge Q must be equal to
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is
An electron moves in a circular arc of radius 10 m at a contant speed of 2 × 107 ms–1 with its plane of motion normal to a magnetic flux density of 10–5 T. What will be the value of specific charge of the electron?
From a 200 m high tower, one ball is thrown upwards with speed of 10 ms-1 and another is thrown vertically downwards at the same speeds simultaneously. The time difference of their reaching the ground will be nearest to



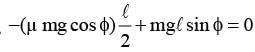
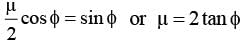
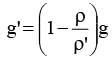
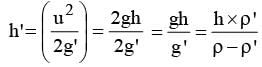
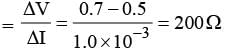
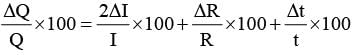
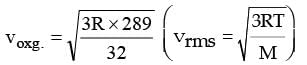
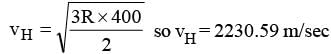
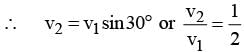
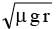
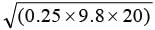 = 7 m / s
= 7 m / s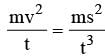
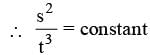
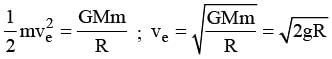
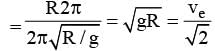

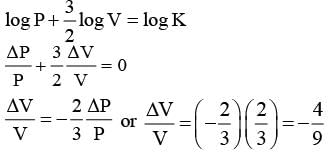
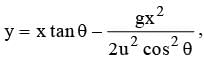 we get tan θ = √3
we get tan θ = √3
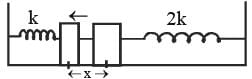
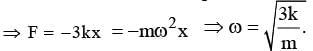
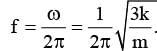
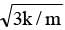

 = -Aω sin (ωt + π/4)
= -Aω sin (ωt + π/4)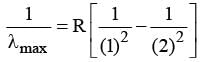

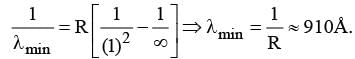
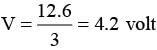
 and for hollow cylinder,
and for hollow cylinder, 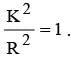 Acceleration down the inclined plane
Acceleration down the inclined plane 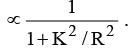 Solid cylin der h as greater acceleration. It reaches the bottom first.
Solid cylin der h as greater acceleration. It reaches the bottom first.