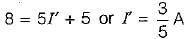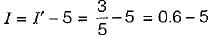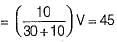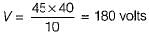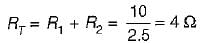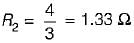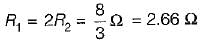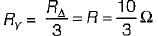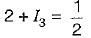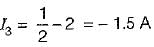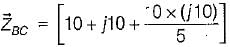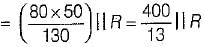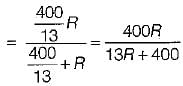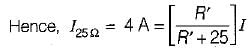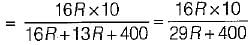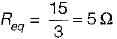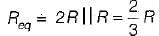Test: Basic Laws- 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: Basic Laws- 2
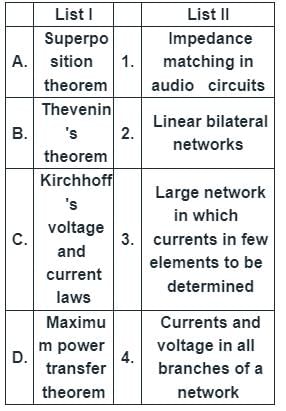
Match List I with List-II and select the correct answer using the code given below the lists:

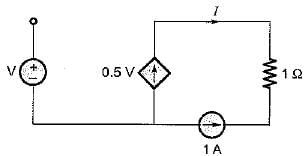
The value of current I in the circuit shown below for V = 2 volt is

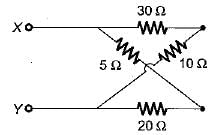
The value of voltage source to be connected across the terminals X and Y so that drop across the 10 Ω resistor is 45 V is
In a voltage divider circuit as shown below with two resistances R1 and R2, the voltage drop V1 is twice the drop V2 across R2. The value of R1, and R2 will be

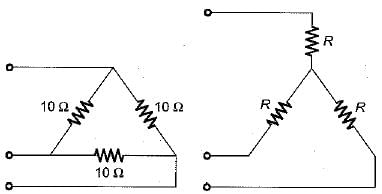
A delta connected load is shown in figure below. The equivalent star connection has a value of R in Ω is
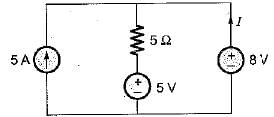
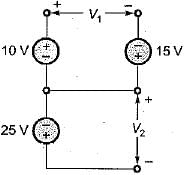
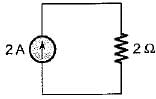
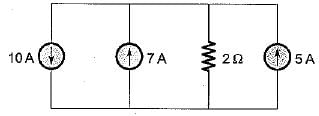
The voltage drop across the 2 Ω resistor for the circuit shown below is
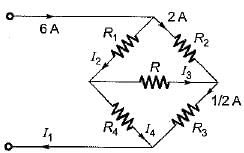
For the circuit shown below, the sum of the unknown currents I1, I2, l3 and I4 is
In the delta equivalent of the given star connected circuit 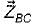 is equal to
is equal to
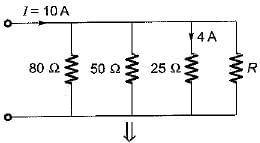
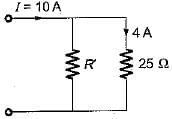
Four resistances 80 Ω, 50 Ω, 25 Ω and R are connected in parallel. Current through 25 Ω resistance is 4 A. The total current of the supply is 10 A. The value of R will be
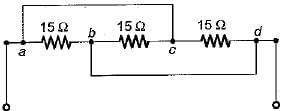
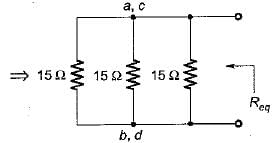
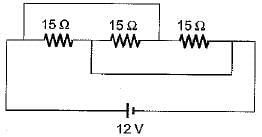
For the circuit shown below, the equivalent resistance will be
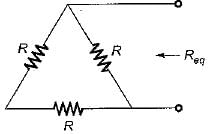
Three resistors of R Ω each are connected to form a triangle. The resistance between any two terminals will be
A network has 10 nodes and 17 branches. The number of different node pair voltage would be