Test: Boolean Operations - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test GATE Computer Science Engineering(CSE) 2025 Mock Test Series - Test: Boolean Operations
Consider a carry look-ahead adder for adding two n-bit integers, built using gates of fan-in at most two. The time to perform addition using this adder is:
Consider an eight-bit ripple-carry adder for computing the sum of A and B, where A and B are integers represented in 's complement form. If the decimal value of A is one, the decimal value of B that leads to the longest latency for the sum to stabilize is ___________
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
An N-bit carry lookahead adder, where N is a multiple of 4, employs ICs 74181 (4 bit ALU) and 74182 ( 4 bit carry lookahead generator).
The minimum addition time using the best architecture for this adder is
The minimum addition time using the best architecture for this adder is
The number of full and half-adders required to add 16-bit numbers is:
A 4-bit carry look ahead adder, which adds two 4-bit numbers, is designed using AND, OR, NOT, NAND, NOR gates only.Assuming that all the inputs are available in both complemented and uncomplemented forms and the delay of each gate is one time unit, what is the overall propagation delay of the adder? Assume that the carry network has been implemented using two-level AND-OR logic.
The maximum gate delay for any output to appear in an array multiplier for multiplying two-bit numbers is:
Consider an array multiplier for multiplying two n bit numbers. If each gate in the circuit has a unit delay, the total delay of the multiplier is:
are Boolean variables,
operator.
Which one of the following must always be TRUE?
The total number of Boolean functions which can be realised with four variables is:
The simultaneous equations on the Boolean variables x, y, z and w,
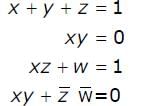
have the following solution for x, y, z and w, respectively:
Consider the Boolean operator # with the following properties :
Find values of Boolean variables A,B,C which satisfy the following equations:
- A+ B = 1
- AC = BC
- A + C = 1
- AB = 0
In boolean algebra, the OR operation is performed by which properties?
The function AB’C + A’BC + ABC’ + A’B’C + AB’C’ is equivalent to
Define the connective
Consider the following expressions
Which of the following is TRUE?
In boolean algebra, the OR operation is performed by which properties?
Which one of the following expressions does NOT represent exclusive NOR of x and y?
denote the exclusive OR (XOR) operation. Let '1' and '0' denote the binary constants. Consider the following Boolean expression for F over two variables P and Q:
The equivalent expression for is
The equivalent expression for F is
If are Boolean variables, then which one of the following is INCORRECT?
Choose the correct alternatives (more than one may be correct) and write the corresponding letters only: The operation which is commutative but not associative is:
When multiplicand Y is multiplied by multiplierusing bit-pair recoding in Booth's algorithm, partial products are generated according to the following table.
The partial products for rows 5 and 8 are
Booth’s algorithm for integer multiplication gives worst performance when the multiplier pattern is
|
55 docs|215 tests
|
|
55 docs|215 tests
|


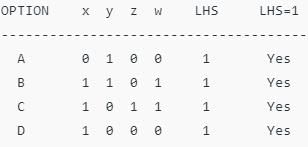 Till now, all the options are possible.
Till now, all the options are possible.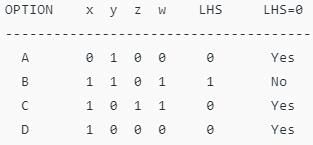 Since LHS ≠ 0, B is not possible.
Since LHS ≠ 0, B is not possible.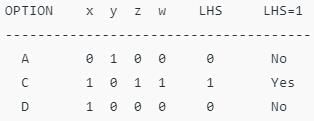 Since LHS ≠ 1, A and D are not possible.
Since LHS ≠ 1, A and D are not possible. Thus, C is the correct option.
Thus, C is the correct option.














