Test: CAT Logical Reasoning & Data Interpretation- 2 - CAT MCQ
20 Questions MCQ Test - Test: CAT Logical Reasoning & Data Interpretation- 2
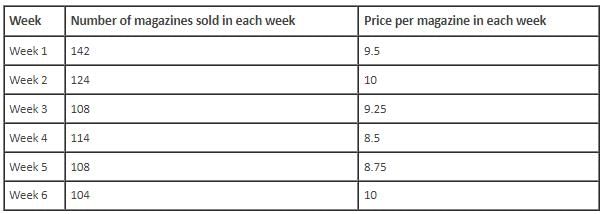
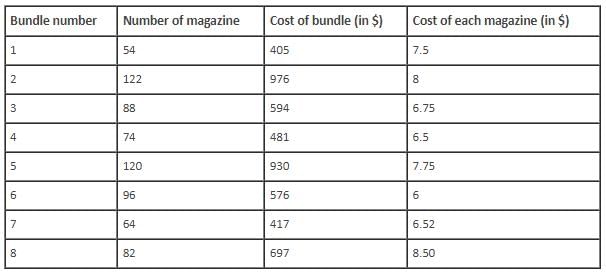
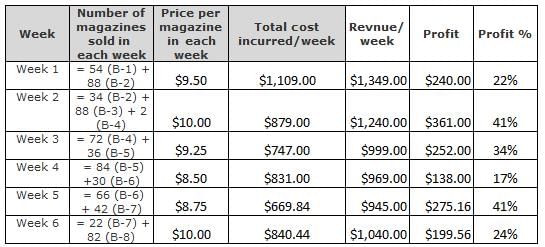
Key in the number of the week in which Mr. Brown made the third highest percent of profit.
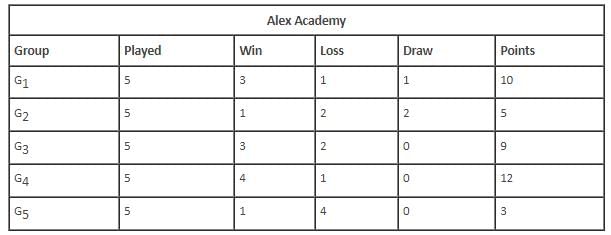
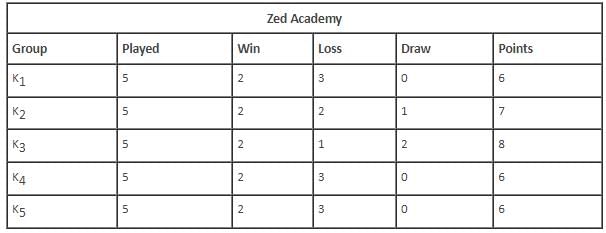
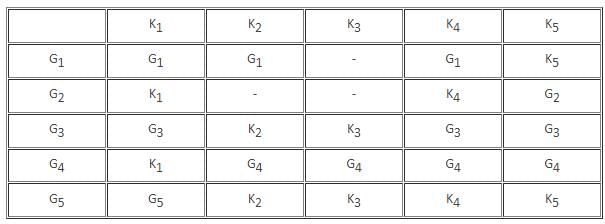
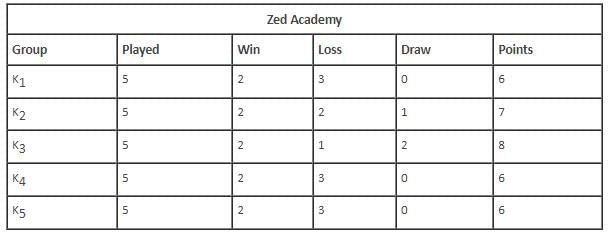
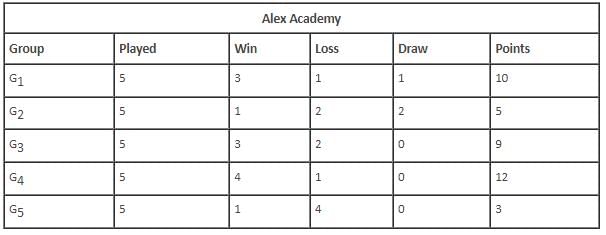
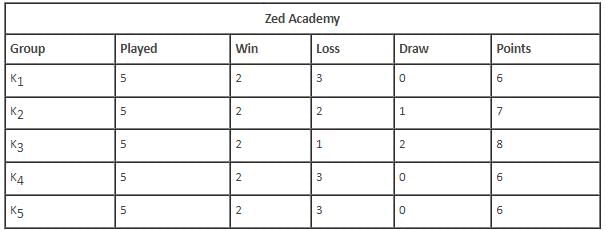
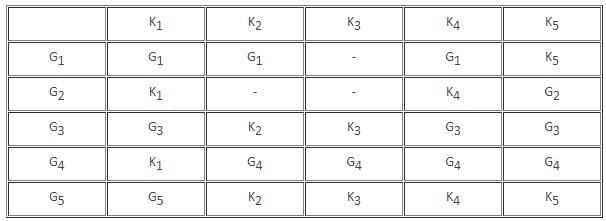
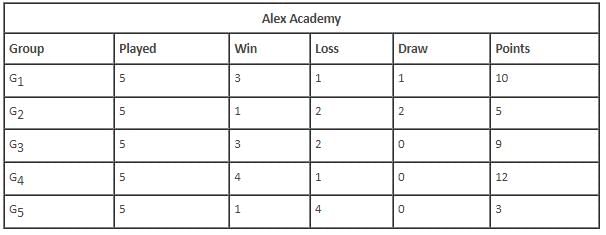
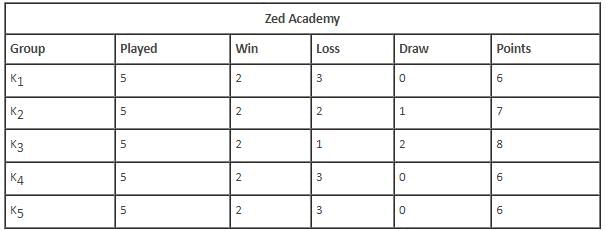
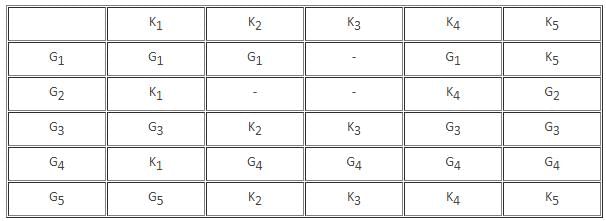
Which of the following groups drew the maximum number of rounds?
K2 lost a round against which of the following groups
The group that scored the least number of points won against which of the following groups?
The total number of rounds that K4 lost was _________.
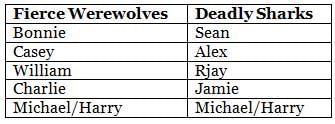
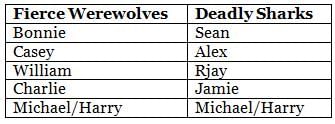
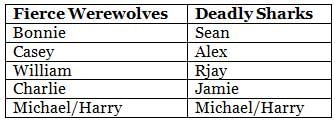
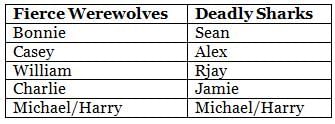
Which among the following is a part of Fierce Werewolves?
Who scored the highest number of goals in Deadly Sharks?
Which of the following pairs of players belongs to the same team?
If the title 'Player of the Game' was awarded to the player from the winning team who scored at least two goals and possessed the ball for the highest duration, who was awarded the Player of the Game?
The second least possession time of a player in the winning team is more or less than the same for a player in the losing team by _______ minutes.
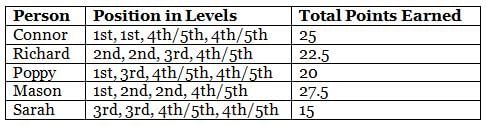
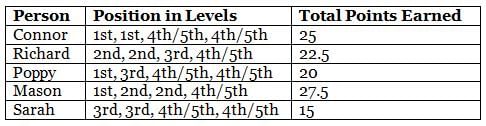
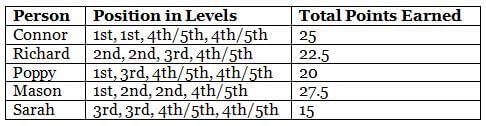
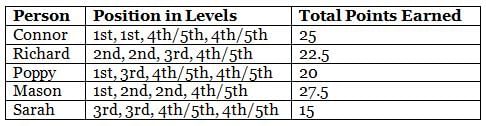
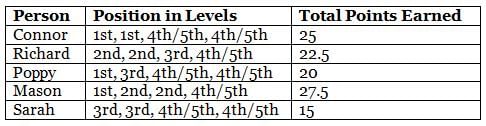
What are the highest points earned by any of the five persons in the game?
Which of the following groups consists of Supervisors?
How many of the following definitely earned higher points than Sarah in at least three of the four levels?
1. Connor
2. Richard
3. Poppy
4. Mason
Who among the following is the Personnel Manager?
Which of the following statements is definitely true?
From which branch does Mr. Dushyant Vaidya operate?
Who scored the first position more than one time in levels?
Which of the following statements is true?
What is the sum of the points earned by Connor, Mason and Sarah?
Which of the following combinations is not true?