Test: CAT Quantitative Aptitude- 4 - CAT MCQ
22 Questions MCQ Test - Test: CAT Quantitative Aptitude- 4
If the sum of the roots of the quadratic equations mx2 + (2m - 1)x + 4 and (3m + 1)x2 - 6x + (2m - 3) are equal, then find the sum of values of m.
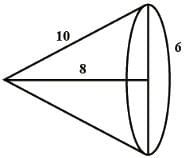
A right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. find the volume of the solid so formed.
The largest integer n, such that n + 10 divides n3 + 100, is
How many subsets of S = (1, 2, 3 , . . . , 400) have the product of their elements an even number?
Find the maximum area of the isosceles trapezium (in units2) whose unequal sides are 4 units and 6 units. Given that it is inscribed in a circle whose radius is 2√3
The average speed of Mumbai metro train which travels from Ghatkopar to Versova is 30 km/hr and the distance between the two stations is 32 km. Which function represents the distance 'd(t)' remaining in a trip from Ghatkopar to Versova after a certain time 't' from the start?
6 equally spaced girls are standing along the circumference of a circle of radius 10 m and facing the center. What is the shortest distance between any two girls facing each other?
Akhsay travels on a straight route joining P and Q in a way such that after each of the 20th, 40th and 60th minute from his starting point P, he increases his speed by 10 kmph and after each of the 70th, 80th, 90th, 100th and the 110th minute from the start, he decreases his speed by 10 kmph. If Akshay began his journey at a speed of 50 kmph and took exactly 2 hours to reach Q, the distance from P to Q (in km) is _______.
A shopkeeper gives a discount of 10% on the marked price and sells it for Rs. 540 to earn a profit of Rs. 90. Find the profit percentage if the product is marked Rs. 200 above its cost price for the same absolute value of discount.
A thief is running on a circular track of radius 5 m at 1.5 m / s . A policeman whose speed is twice that of the thief arrived at the starting point of the track 4 seconds after the thief. The policeman can either run along the circular track in the direction of the thief or go to the centre and then go to any point on the circle from the centre. Find the minimum distance covered by the thief after the policeman starts chasing him.
If x = 44 x 56 x 65 x 710 x 88, then how many factors of x are of the form 6 A2?
x is a positive integer with value at most equal to 110. How many values of x are possible if x is not a factor of (x - 1)!?
The speed of a boat in still water is 24 kmph. If it can travel 20 km downstream in the same time as it can travel 12 km upstream, then it is ______ times as fast as the stream. Key in the number.
Find the minimum value of the quadratic expression 3x2 + 11x - 23.
50 square stone slabs of equal size were needed to cover, a floor area of 72 sq. m. The length of each stone slab is :
37% of the total number of people in a city read newspaper ABC and exceed the number of people who read XYZ by 8000. If 27% of the total population do not read any newspaper then find the population of the city if there are only two newspapers in the city. [Assume that no one reads more than one newspaper].
If x2 + x - 2 < 0; then which of the following statement is true?
1. x - 1 > 0
2. x - 1 < 0
3. x + 2 > 0
4. x - 2 < 0
At 12:00 AM both the hour and a minute hand were overlapping each other. How many more minutes does the minute hand travel than the hour hand in the next 54 minutes?
A and B start working together on a project and both have the same efficiency in the beginning. However the efficiency of A decreases to 0.6 times the usual after working for 2 hours. If the project can be finished in 120 man hours, then find the minimum number of days required to finish the work if both do an equal manhours of work each day and the sum of the total number of hours of work by both each day is 12. [ Initial efficiency of A = Efficiency of B = 1 man hour].
The average number of apples per carton for three cartons of apple is 90. The average price per carton is Rs.1500. The average price of apples in the two cartons which do not contain the highest number of apples is 20 and 25 respectively. The price of the carton with the highest number of apples is 1900. If the highest difference in the number of apples in any two cartons is 100, then find the lowest number of apples in a carton.
A saree is one-fourth by length green, two-fifth by length red and the remaining 3850 cm by length is black. What is the length of the saree in meters?