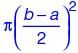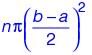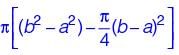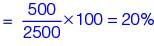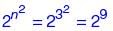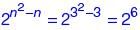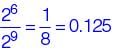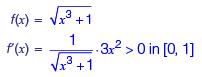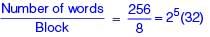Test : CSE Past Year Paper 2020 - GATE MCQ

Two straight lines are drawn perpendicular to each other in X-Y plane. If α and β are the acute angles the straight lines make with the X-axis, then α + β is ________.

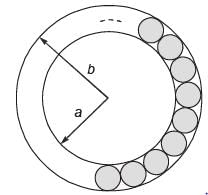
The figure below shows an annular ring with outer and inner radii as b and a, respectively.
The annular space has been painted in the form of blue colour circles touching the outer and inner periphery of annular space. If maximum n number of circles can be painted, then the unpainted are available in annular space is ________.

There are multiple routes to reach from node 1 to node 2, as shown in the network.

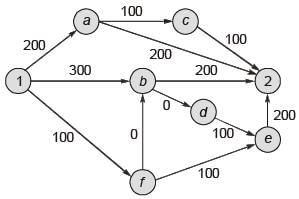
The cost of travel on an edge between two nodes is given in rupees. Nodes ‘a’ ‘b’, ‘c’, ‘d’, ‘e’ and ‘f’ are toll booths. The toll price at toll booths marked ‘a’ and ‘c’ is Rs. 200. and is Rs. 100 for the other toll booths. Which is the cheapest route from node 1 to node 2?

His knowledge of the subject was excellent but his classroom performance was ________.

Select the word that fits the analogy:
Cook : Cook :: Fly : ________

The dawn of the 21st century witnessed the melting glaciers oscillating between giving too much and too little to billions of people who depend on their for fresh water. The UN climate report estimates that without deep cuts to man-made emissions, at least 30% of the northern hemisphere’s surface permafrost could melt by the end of the century.Given this situation of imminent global exodus of billions of people displaced by rising seas, nation-states need to rethink their carbon footprint for political concerns, if not for environmental ones.
Which one of the following statements can be inferred from the given passage?

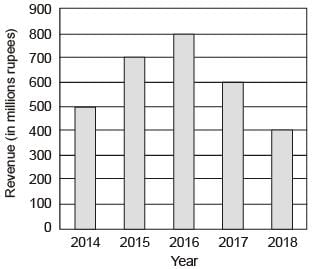
The total revenue of a company during 2014-2018 is shown in the bar graph. If the total expenditure of the company in each year is 500 million rupees, then the aggregate profit loss (in percentage) on the total expenditure of the company during 2014-2018 is ________.

Let R be the set of all binary relations on the set {1, 2, 3}. Suppose a relation is chosen from R at random. The probability that the chosen relation is reflexive (round off to 3 decimal places) is ________.

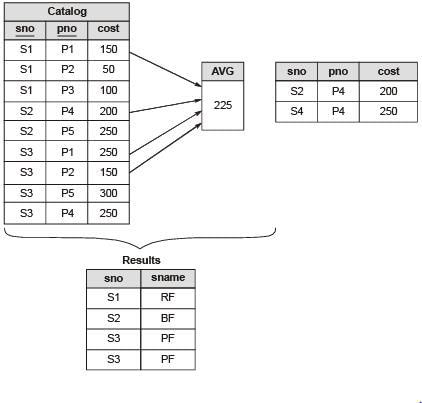
Consider a relational database containing the following schemas.



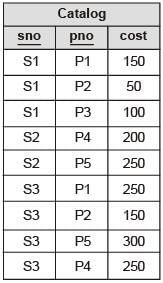
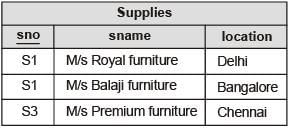
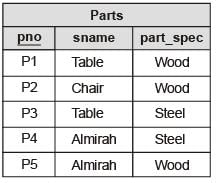
The primary key of each table is indicated by underlining the constituent fields.

The number of rows returned by the above SQL query is

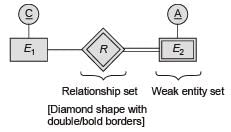
Which one of the following is used to represent the supporting many-ore relationships of a weak entity set in an entity-relationship diagram?

Consider allocation of memory to a new process. Assume that none of the existing holes in the memory will exactly fit the process’s memory requirement. Hence, a new hole of smaller size will be created if allocation is made in any of the existing holes. Which one of the following statements is TRUE?

What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order?

Consider the following C program:

The output of the program is ________.

Consider the functions: 
I. e^-x
II. x² – sin x
III.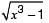 
Which of the above functions is/are increasing everywhere in [0,1]?

Consider the following statements about process state transitions for a system using preemptive scheduling.
I. A running process can move to ready state.
II. A ready process can move to running state.
III. A blocked process can move to running state.
IV. A blocked process can move to ready state.
Which of the above statements arc TRUE?

Consider the following statements:
I. If L₁ ∪ L₂ is regular, then both L₁ and L₂ must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?

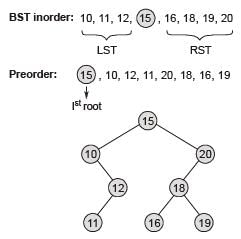
The preorder traversal of a binary search tree is 15, 10. 12, 11, 20, 18,  16, 19. Which one of the following is the postorder traversal of the tree?

Consider the following grammar:
S → aSB⏐d
B → b
The number of reduction steps taken by a bottom-up parser while accepting the string aaadbbb is ________.

Which one of the following regular expressions represents the set of all binary strings with an odd number of 1’s?

What is the worst case time complexity of inserting n² elements into an AVL-tree with n elements initially?

Consider the language L = {aⁿ⏐n > 0} ∪ {aⁿbⁿ⏐n ≥ 0} and the following statements.
I. L is deterministic context-free.
II. L is context-free but not deterministic context-free.
III. L is not LL(k ) for any k.
Which of the above statements is/are TRUE?

A multiplexer is placed between a group of 32 registers and an accumulator to regulate data movement such that at any given point in time the content of only one register will move to the accumulator, The minimum number of select lines needed for the multiplexer is _________.

If there are m input lines and n output lines for a decoder that is used to uniquely address a byte addressable 1 KB RAM, then the minimum value of m + n is ________.

A direct mapped cache memory of 1 MB has a block size of 256 bytes. The cache has an access time of 3 ns and a hit rate of 94%. During a cache miss, it takes 20 ns to bring the first word of a block from the main memory, while each subsequent word takes 5 ns. The word size is 64 bits. The average memory access time in ns (round off to 1 decimal place) is ________.

Consider a double hashing scheme in which the primary hash function is h₁(k) = k mod 23 and the secondary hash function is h₂(k) = 1 + (k mod 19). Assume that the table size is 23. Then the address returned by probe 1 in the probe sequence (assume that the probe sequence begins at probe 0) for key value k = 90 is ________.

Consider the following statements about the functionality of an IP based router.
I. A router does not modify the IP packets during forwarding.
II. It is not necessary for a router to implement any routing protocol.
III. A router should reassemble IP fragments if the MTU of the outgoing link is larger than the size of the incoming IP packet.
Which of the above statements is/are TRUE?

Consider the following data path diagram.

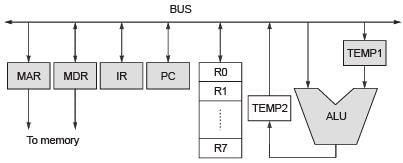
Consider an instruction: R0 ← R1 + R2. The following steps are used to execute it over the given data path. Assume that PC is incremented appropriately. The subscripts r and w indicate read and write operations, respectively.
1. R2_r, TEMP1_r, ALU_add, TEMP2_w
2. R1_r, TEMP1_w
3. PC_r, MAR_w, MEM_r
4. TEMP2_r, R0_w
5. MDR_r, IR_w
Which one of the following is the correct order of execution of the above steps?