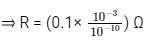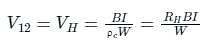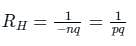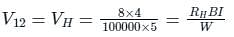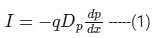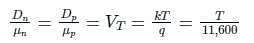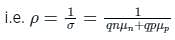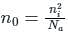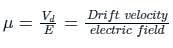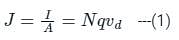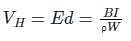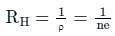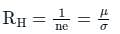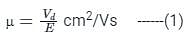Test: Carrier Transport - 1 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Carrier Transport - 1
Gradual flow of charge from a region of high density to a region of low density is called _________.
An n–type silicon sample of 10–3 m length and 10–10 m2 cross sectional area has an impurity concentration of 5 × 1020 atom/m3. If mobility of majority carries is 0.125 m2/v-sec, then the resistance of the sample will be ________.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Calculate the hall voltage when the magnetic field is 8 A/m, current is 4 A, width is 5 m and the concentration of carrier is 100000.
According to Einstein’s relationship for a semiconductor, the ratio of the diffusion constant to the mobility of the charge carriers is
Electric Field of 1 V/m is applied to a Boron doped Silicon semiconductor slab having a doping density of 1016 atoms/cm3 at 300 K temperature. Determine the approximate resistivity of the slab.
(Consider intrinsic carrier concentration of Silicon at 300 K = 1.5 × 1010 /cm3; Hole Mobility = 500 cm2/Vs at 300 K; Electron Mobility = 1300 cm2/Vs at 300 K).
If temperature will increase, the conductivity of semiconductor will:
On applying an electric field of intensity 10 V/cm across a semiconductor at a certain temperature the average drift velocity of free electrons is measured to be 70 m/s. Then the electron mobility is
|
25 docs|263 tests
|
|
25 docs|263 tests
|