Test: Cartesian Vectors - Mechanical Engineering MCQ
30 Questions MCQ Test - Test: Cartesian Vectors
In right handed coordinate system which axis is considered to be positive?
If A is any vector with Ai + Bj + Ck then what is the y-axis component of the vector?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If the force vector F is having its x-axis component being equal to Z N, y-axis component be X N and z-axis component be Y N then vector F is best represented by?
Which statement is right for force vector F = Ai + Bj + Ck?
What is the magnitude of the Cartesian vector having the x, y and z axis components to be A, B and C?
What is cosα for force vector F = Ax + By +Cz (Given α, β and γ are the angles made by the vector with x, y and z axis respectively) ?
What is the sum of squares of the cosine angles made by the force vector with the coordinate axis?
What is x-axis component of the force vector Ai + Bj +Ck with magnitude equal to F?
We can add the force vectors directly. But with dividing each by it’s magnitude first. (True/False)
For a vector F, Fcosβ is equal to zero. What does this refer?
Find the angle α, for the vector making an angle by y and z axis as 60˚ and 45˚ respectively. It makes an angle of α with x-axis. The magnitude of the force is 200N.
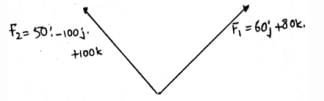
What is the magnitude of the resultant force when F1 = 60j + 80k and F2 = 50i – 100j + 100k?
Express F = 100 N (shown in the figure below) as a Cartesian vector.
Express the vector in the Cartesian Form, if the angle made by it with y and z axis is 60˚ and 45˚ respectively. Also it make an angle of α with x-axis. The magnitude of the force is 200N.
In the figure given below, with F1 = 60j + 80k and F2= 50i -100j + 100k, what is the value of β? (β is the angle made by the resultant vector with the y-axis)
In the figure given below, calculate the value of cosγ. (γ is the angle made by the resultant vector and the z-axis)
The coordinate of the Force vector AB is A (2, 0, 2) and B (-2, 3.46, 3). What are its directions?
The coordinate of the Force vector AB is A (2, 0, 2) and B (-2, 3.46, 3). It has a magnitude of 750N. Which is the best Cartesian representation of the vector AB?
A force vector is along 4i – 4k direction and has a magnitude 100N and another force vector is along 4i +2j -4k and has a magnitude of 120N. What is the resultant of both forces?
The value cos-1(-3/7) + cos-1(2/7) + cos-1(6/7) is ____________
Two vectors emerging from a point are always in a single plane.
Three vectors emerging from a point are always in a single plane.
What is the difference between position vector and unit vector?
Which is true for the vector provided only position coordinates given?

















