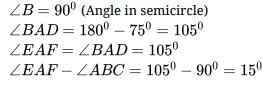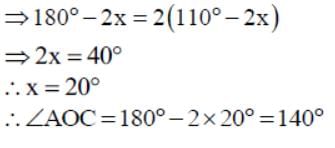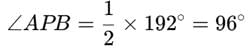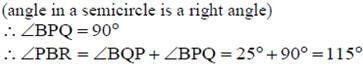Test: Circles- 2 - Grade 9 MCQ
25 Questions MCQ Test - Test: Circles- 2
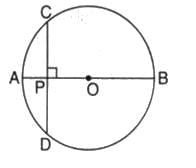
AB is a chord of a circle with radius ‘r’. If P is any point on the circle such that ∠APB is a right angle , then AB is equal to
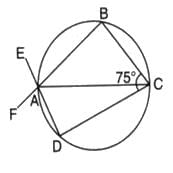
In the given figure, AC is a diameter of the given circle and ∠BCD = 75o. Then, ∠EAF−∠ABC is equal to

P is a point on the diameter AB of a circle and CD is a chord perpendicular to AB. If AP = 4 cm and PB = 16 cm, the length of chord CD is
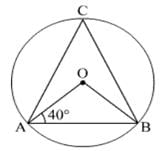
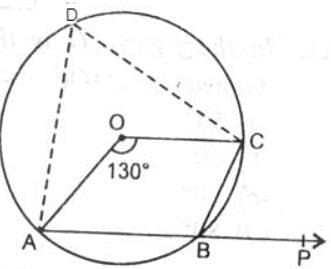
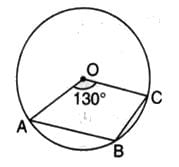
Arc ABC subtends an angle of 130o at the centre O of the circle. AB is extended to P. Then ∠CBP equals :
Chords AB and CD intersect at right angles. If ∠BAC = 40o, then ∠ABD is equal to
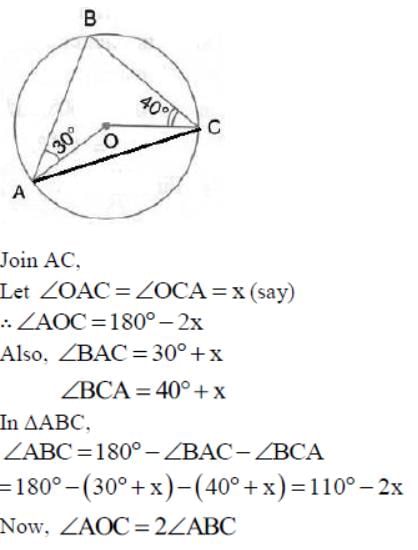
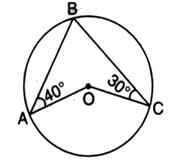
In the given figure, O is the centre of the circle. ∠OAB and ∠OCB are 40o and 30o respectively. Then, the measure of ∠AOC is
In the given, AB is side of regular five sided polygon and AC is a side of a regular six sided polygon inscribed in the circle with centre O. AO and CB intersect at P, then ∠APB is equal to
In the given figure, if ∠AOB = 80o and ∠ABC = 30o , then ∠CAO is equal to
In the figure, O is the centre of eh circle and ∠AOB = 80o. The value of x is :
In the given figure if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to
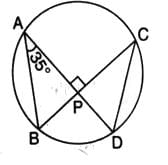
Chords AD and BC intersect each other at right angles at point P. ∠DAB = 35o, then ∠ADC is equal to
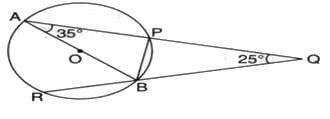
In the given figure, AB is a diameter of the circle APBR. APQ and RBQ are straight lines. If ∠A = 35o and , then the measure of ∠PBR is
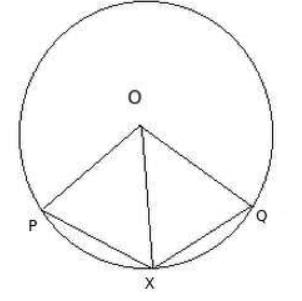
X is a point on a circle with centre O. If X is equidistant from the two radii OP, OQ, then arc PX : arc PQ is equal to
BC is a diameter of the circle and ∠BAO = 60o . Then ∠ADC is equal to
What fraction of the whole circle is minor arc RP in the given figure ?
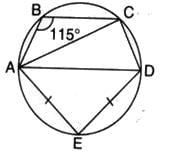
In the given figure, AD is the diameter of the circle and AE = DE. If ∠ABC = 115o, then the measure of ∠CAE is
In the figure, if ∠DAB = 60o, ∠ABD = 50o, then ∠ACB is equal to :
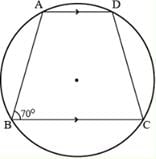
If ABCD is a cyclic trapezium in which AD ║ BC and ∠B = 70o, determine other three angles of the trapezium.
In the given figure, O is the centre of the circle and ∠AOC = 130o. Then ∠ABC is equal to
In the given circle, O is the centre and ∠BDC = 42o. Then, ∠ACB is equal to
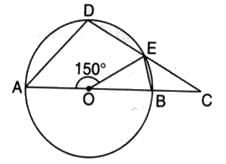
AOB is the diameter of the circle. If ∠AOE = 150o, then the measure of ∠CBE is
In the given figure, a circle is centred at O. The value of x is :
In a circle, if the length of the chord AB is 12 cm and the perpendicular distance from the center O to the chord AB is 5 cm, what is the radius of the circle?