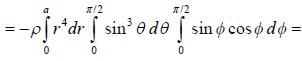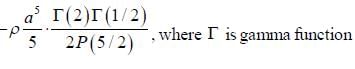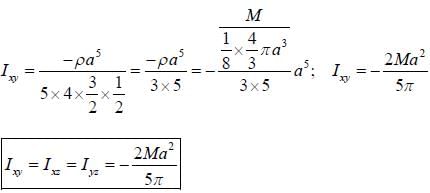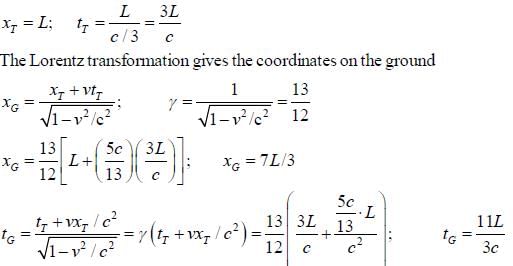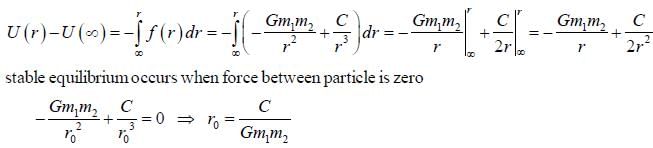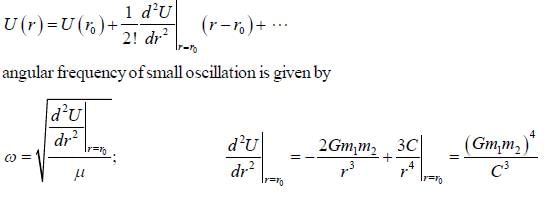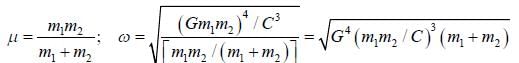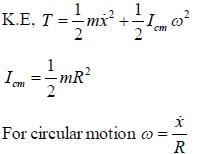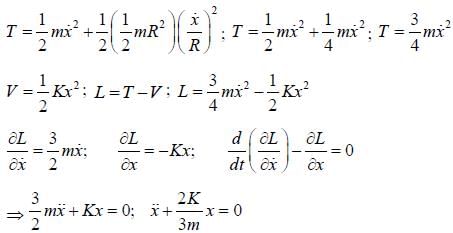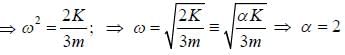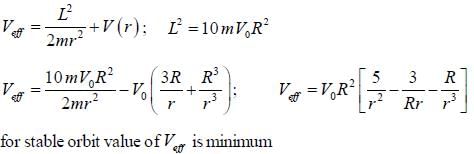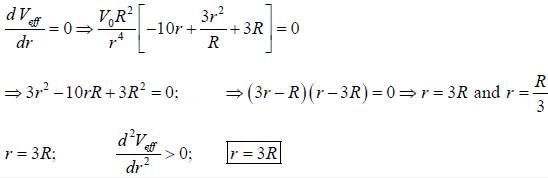Test: Classical Mechanics - 1 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: Classical Mechanics - 1
Consider a satellite in a circular orbit around the earth. Then properties of the satellite depend on the radius of the orbit r as follows: speed 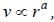 time period
time period 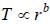 angular momentum
angular momentum 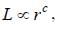 and kinetic energy
and kinetic energy 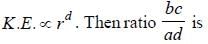
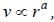 time period
time period 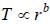 angular momentum
angular momentum 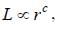 and kinetic energy
and kinetic energy 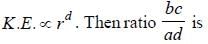
For streamline motion of an incompressible non-viscous fluid, is states by Bernoulli’s principle ____.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A particle is placed in a region with the potential 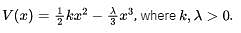
Then,
A bullet is fired horizontally in the north direction with a speed u at θ latitude. It hits a target 1 meter away. Calculate the Coriolis acceleration.
If a spring of spring constant k is stretched by x0, the work done is W0. Now, a second spring of spring constant 3k is stretched by x0/3. The work done is 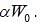 The value of a is _____ (Correct upto two decimal place).
The value of a is _____ (Correct upto two decimal place).
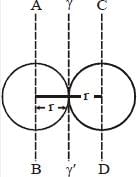
The moment of inertia of pairs of solid sphere each having mass m radius r kept in contact about a tangent passing through the point of contact is βmr2. The value of β is ______ . (Upto one decimal place)
The moment of inertia tensor of a rigid body is given by
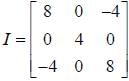
Moment of inertia about an axis 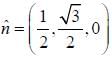 is _______.
is _______.
A uniform chain of length L and mass M is lying on a smooth table and one third of its length is hanging vertically down over the edge of the table. The work required to pull the hanging part on the table is 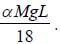 The value of α is _________
The value of α is _________
The Hamiltonian of a system is given by
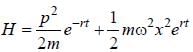
It describes the motion of
The muon is an unstable particle that spontaneously decay into an electron and two neutrinos if the number of muons at t = 0 is N0, 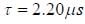 is the mean life time of muon. Suppose muons move at speed 0.95c, the number of muons remain after travelling a distance of 3.0 km is _______ (in terms of N0) (upto three decimal places)
is the mean life time of muon. Suppose muons move at speed 0.95c, the number of muons remain after travelling a distance of 3.0 km is _______ (in terms of N0) (upto three decimal places)
A comet in an orbit about the sun has a velocity 10km/sec at aphelion and 80km/sec at perihelion if the earth's velocity in a circular orbit is 30 km/sec and the radius of its orbit is 1.5 x 108km, the aphelion distance Ra for comet is ____ x 108km. (Nearest integer)
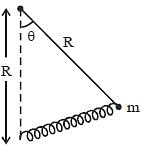
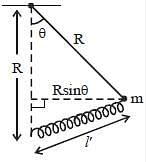
Find Lagrangian of the pendulum of mass m and length R attached to a spring, the other end of which is fixed at the bottom as shown in the figure. The length of the undeformed spring is l
The kinetic energy of a particle in terms of coordinate r and q = sin θ, where r & θ are polar coordinate is
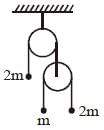
Consider the At wood's machine. Let x and y be the vertical position of the middle mass and right mass, respectively with upward taken to be positive. The conjugate momenta, Px and Py respectively, are
If Iij is the tensor of inertia of a solid sphere, x2+y2+z2 = a2, of mass M in the first octant, then
A train with proper length L moves with speed 5c/13 with respect to the ground. A ball is thrown from the back of the train to the front. The speed of the ball with respect to the train is c/3. As viewed by someone on the ground how much time does the ball spend in the air and how far does it travel.
The force of interaction between a particle of mass m1 and a second particle of mass m2 separated by a distance r is given by an attractive gravitational force and a repulsive force that is proportional to r-3, with probability constant C,
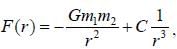
the angular frequency of small oscillation about the stable equilibrium position is
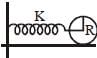
A disk of mass m and radius R is attached to a spring of constant K as shown in the figure. The disk rolls and forth without slipping. The angular frequency of the motion of the disk is 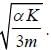 The value of α is ______.
The value of α is ______.
The particle of mass m and angular momentum L2 = 10mV0R2 moves in a potential
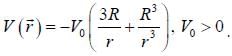
The radius of the stable circular orbit is _____R.
|
1 docs|34 tests
|




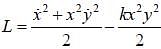
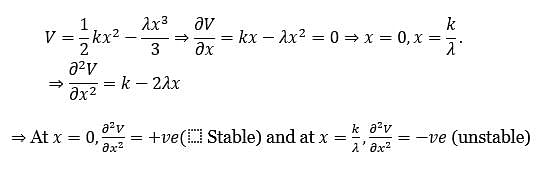
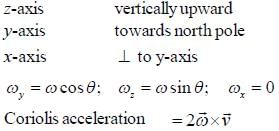
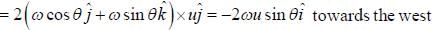
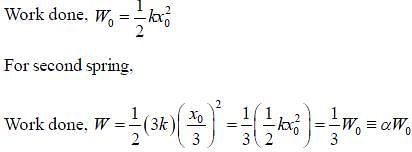
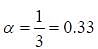
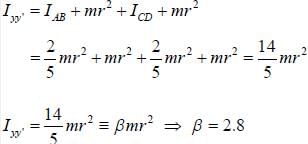
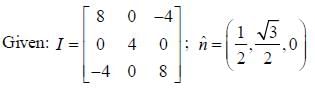
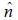
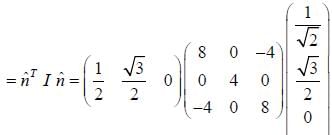
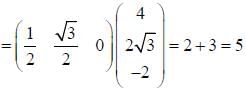
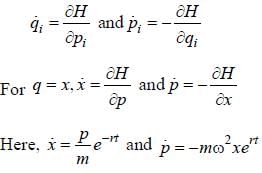

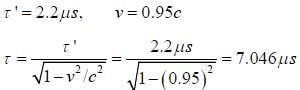

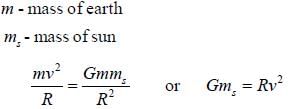
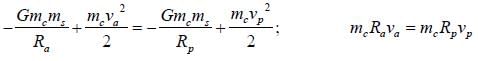

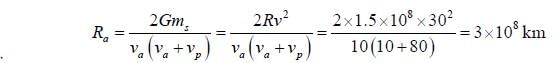
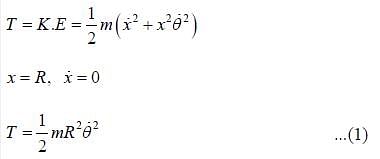
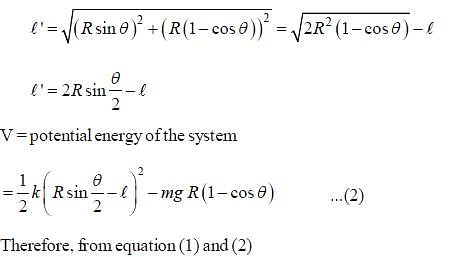
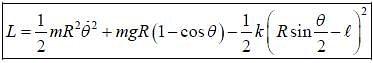
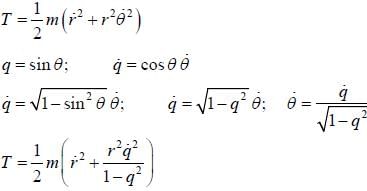

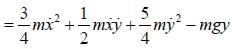
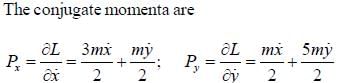
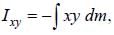 dm = pdx dy dz
dm = pdx dy dz