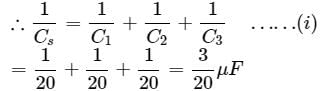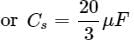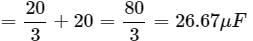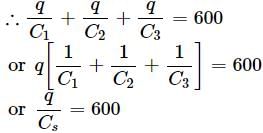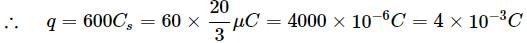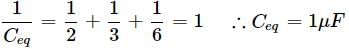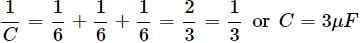Test: Combination of Capacitors (NCERT)
10 Questions MCQ Test Topic-wise MCQ Tests for NEET | Test: Combination of Capacitors (NCERT)
Three capacitors each of capacity 4 μF are to be connected in such a way that the effective capacitance is 6 μF. This can be done by
To get equivalent capacitance 6 μF. Out of the 4 μF capacitance, two are connected in series and third one is connected in parallel.
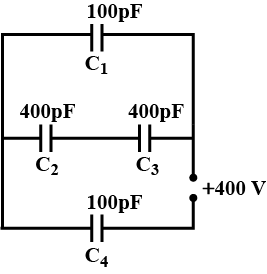
The equivalent capacitance for the network shown in the figure is
Capacitance of C1 = C4 = 100pF
Capacitance of C2 = C3 = 400pF
Supply voltage , V = 400V
Capacitors C2 and C3 are connected is series,
Equivalent capacitance 
Capacitors C1 and C are in parallel
Their equivalent capacitance.
C = C + C1 = 200 + 100 = 300pF
Capacitors C'' and C4 are connected in series Equivalent capacitance
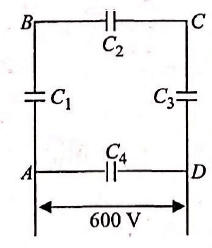
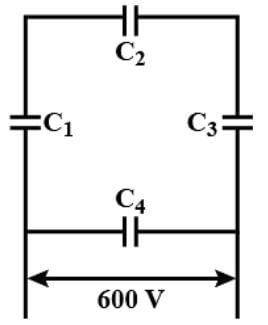
A network of four 20μF capacitors is connected to a 600V supply as shown in the figure.
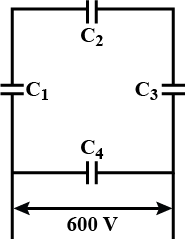
The equivalent capacitance of the network is
The equivalent capacitance of the network is
Form the figure C1, C2, C3 are connected in series.
Now Cs is in parallel with C4
∴ equivalent capacitance Ceq = Cs + C4
The charge on capacitors C1 and C4 are
Charge on each capacitor C1, C2, C3 is same = q
Let charge on C4 be q.
Also qC4 = 600
or q = C4 × 600μC = 20 × 600μC = 12 × 10−3C
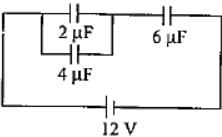
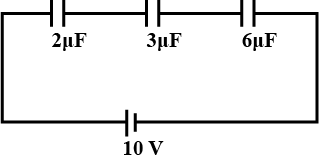
The charge on 3μF capacitor shown in the figure is
Since all the capacitors are connected in series,
∴ equivalent capacitance is
Charge on each capacitor is same (∵ V = 10V)
q = CeqV = 1 × 10 = 10μC
Minimum number of capacitors each of 8μF and 250V used to make a composite capacitor of 16μF and 1000V are
Minimum number of capacitors in each row = 1000/250 = 4
Therefore, 4 capacitors connected in series.
If there are m such rows, that total capacity
= m × 2 = 16 ∴ m = 16/28
∴ minimum number of capacitors = 4 × 8 = 32
A capacitor of capacitance C1 is charged to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The final potential difference across each capacitor will be
When a charged capacitor of capacitance C1 is connected in parallel to an uncharged capacitor of capacitance C2, the charge is shared between them till both attain the common potential which is given by, common Potential = q1 + q2/C1 + C2 = q1 + q2/C1 + C2 = C1V/C1 + C2
Two capacitors of 2 μF and 4 μF are connected in parallel. A third capacitor of 6 μF is connected in series. The combination is connected across a 12 V battery. The voltage across 2 μF capacitor is
Cp = 2 + 4 = 6μF
Total Q = CV = 3 × 12 = 36μF
Voltage across 6μF capacitor = 36μC/6μF = 6V
∴ Voltage across each of 2μF and 4μF capacitors = 12V - 6V
V = 6V
Two identical capacitors are joined in parallel, charged to a potential V, separated and then connected in series, the positive plate of one is connected to the negative of the other. Which of the following is true?
When the two capacitors charged to same potential are connected in series, then total potential difference V′ = V1 + V2 = V + V = 2V
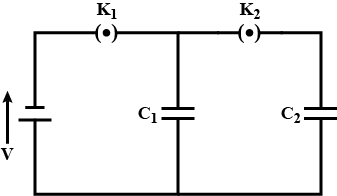
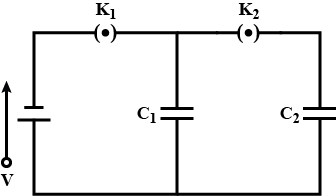
In the given circuit, initially K1 is closed and K2 is open. Then K1 is opened and K2 is closed. If q1′ and q2′ are charges on C1 and C2 and V1 and V2 are the voltage respectively, then
From the figure, when K1 is closed and K2 is open, C1 is charged to potential V acquiring a total charge q = C1V When K1 is open and K2 is closed, battery is cut off C1 and C2 are in parallel. The charge on C1 is shared between C1 and C2 such that V1 = V2
As there is no loss of charge q1′ + q2′ = q
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
 |
|
 |
 |
 |
|
 |
|
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
How to Prepare for NEET
Download free EduRev App
Similar Content
 |
 |
|
 |
|
 |
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|