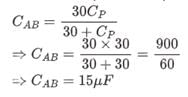Test: Combination of Capacitors - JEE MCQ
10 Questions MCQ Test - Test: Combination of Capacitors
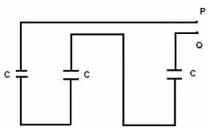
Here is a combination of three identical capacitors. If resultant capacitance is 1 μƒ, calculate capacitance of each capacitor.

If the potential difference of a 6µF capacitor is changed from 10V to 20V, the increase in energy stored will be
If two spheres of different radii have equal charge, then the potential will be
The capacitor preferred for high-frequency circuit is
Three different capacitors are connected in series, then:
There are three capacitors with equal capacitance. In series combination, they have a net capacitance of C1 and in parallel combination, a net capacitance of C2.What will be the value of ratio of C1 & C2?
Two capacitors of 20 μƒ and 30 μƒ are connected in series to a battery of 40V. Calculate charge on each capacitor.
Two capacitors of equal capacity are first connected in series and then in parallel. The ratio of the total capacities in the two cases will be
When two capacitors C1 and C2 are connected in series and parallel, their equivalent capacitances comes out to be 3μƒ and 16μƒ respectively. Calculate values of C1 and C2.
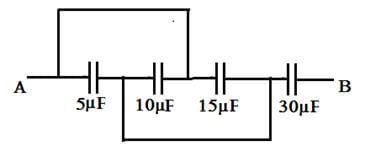
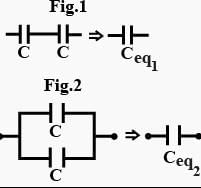
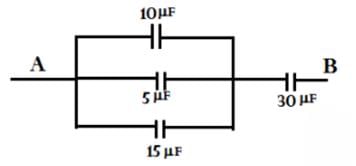
The equivalent capacitance between points A and B in the below shown figure will be ______ μF.