Test: Combinatory- 2 - Computer Science Engineering (CSE) MCQ
25 Questions MCQ Test - Test: Combinatory- 2
In how many ways can three person, each throwing a single die once, make a score of 11
Match the pairs in the following questions by writing the corresponding letters only.

It is required to divide the members of a club into disjoint teams of 2 members each. The teams are not labelled. The number of ways in which this can be done is:
In how many ways can the letters of the word ABACUS be rearranged such that the vowels always appear together?
How many sub strings of different lengths (non-zero) can be found formed from a character string of length n ?
Find the number of binary strings w of length 2n with an equal number of 1's and 0's and the property that every prefix of w has at least as many 0's as 1's.
Let A be a sequence of 8 distinct integers sorted in ascending order. How many distinct pairs of sequences, B and C are there such that
i. each is sorted in ascending order,
ii. B has 5 and C has 3 elements, and
iii. the result of merging B and C gives A
n couples are invited to a party with the condition that every husband should be accompanied by his wife. However, a wifeneed not be accompanied by her husband. The number of different gatherings possible at the party is
m identical balls are to be placed in n distinct bags. You are given that m > kn, where is a natural number > 1. In howmany ways can the balls be placed in the bags if each bag must contain at least balls?
Mala has the colouring book in which each English letter is drawn two times. She wants to paint each of these 52 prints with one of k colours, such that the colour pairs used to colour any two letters are different. Both prints of a letter can also be coloured with the same colour. What is the minimum value of k that satisfies this requirement?
Suppose that a robot is placed on the Cartesian plane. At each step it is allowed to move either one unit up or one unit right, i.e., if it is at then it can move to either
How many distinct paths are there for the robot to reach the point (10,10) starting from the initial position (0,0)?
The number of binary strings of zeros and ones in which no two ones are adjacent is
Two girls have picked 10 roses, 15 sunflowers and 15 daffodils. What is the number of ways they can divide the flowers among themselves?
A pennant is a sequence of numbers, each number being 1 or 2. An -pennant is a sequence of numbers with sum equal to n For example, (1,1,2) is a 4-pennant. The set of all possible 1-pennants is (1), the set of all possible 2-pennants is (2), (1,1) and the set of all 3-pennants is (2,1), (1,1,1,), (1,2). Note that the pennant (1,2) is not the same as thepennant (2,1). The number of 10-pennants is________
The number of 4 digit numbers having their digits in non-decreasing order (from left to right) constructed by using the digits belonging to the set {1, 2, 3} is ________.
The number of substrings (of all lengths inclusive) that can be formed from a character string of length n is
In how many ways can b blue balls and r red balls be distributed in n distinct boxes?
In how many ways can we distribute 5 distinct balls, B1, B2, ..., B5 in 5 distinct cells, C1, C2, ...., C5 such that Ball Bi is not in cell and each cell contains exactly one ball?
A line L in a circuit is said to have a stuck-at-0 fault if the line permanently has a logic value 0. Similarly a line L in a circuit is said to have a stuck-at-1 fault if the line permanently has a logic value 1. A circuit is said to have a multiple stuck-at fault if one or more lines have stuck at faults. The total number of distinct multiple stuck-at faults possible in a circuit with N lines is
Consider the recurrence relation a1 = 8, an = 6n2 + 2n + an-1. Let a99 = K x 104 . The value of K is __________.
Let an be the number of -bit strings that do NOT contain two consecutive 1s. Which one of the following is the recurrence relation for an?
Consider the sequence S0,S1,S2,.... defined as follows: S0 = 0, S1 = 1 and Sn = 2Sn-1 + Sn-2 for n > 2. Which of the following statements is FALSE?
Consider the sequence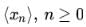 defined by the recurrence relation
defined by the recurrence relation 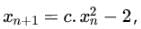 where c >0.
where c >0.
Suppose there exists a non-empty, open interval (a,b) such that for all satisfying a < x0 < b , the sequence converges to a limit. The sequence converges to the value?
Let H1, H2, H3, ... be harmonic numbers. Then, for can be expressed as



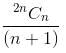 which is the Catalan number.
which is the Catalan number.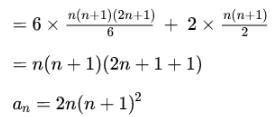 for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104
for n = 99 a99 = 2 x 99 x (99+1)2 = 198 x 104















