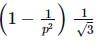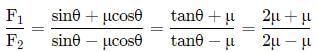Test: Common Forces in Mechanics (NCERT) - NEET MCQ
15 Questions MCQ Test NCERTs at Fingertips: Textbooks, Tests & Solutions - Test: Common Forces in Mechanics (NCERT)
Which of the following statements is correct about friction?
Which of the following is a self adjusting force?
Which one of the following can also act as a lubricant in machines?
A girl presses her physics textbook against a rough vertical wall with her hand. The direction of the frictional force on the book exerted by the wall is:
A car accelerates on a horizontal road due to the force exerted by
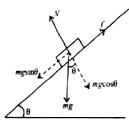
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination theta of the plane to the horizontal will the block just start to slide down the plane?
When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time 20s. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it takes time 20p s, where p is some number greater than 1. The coefficient of friction between the body and the rough plane is
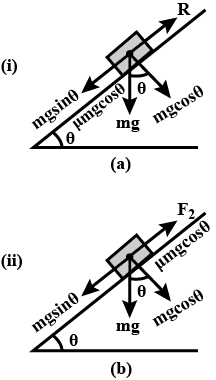
The minimum force required to start pushing a body up a rough (frictional coefficient μ) inclined plane is F1 while the minimum force needed to prevent it from sliding down is F2. If the inclined plane makes an angle θ from the horizontal such that tan θ = 2μ then the ratio F1/F2 is :
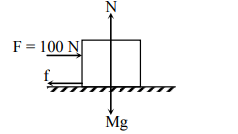
A block of mass 10kg is placed on rough horizontal surface whose coefficient of friction is 0.5. If a horizontal force of 100N is applied on it, then acceleration of the block will be(Take g = 10 m s-2)
The coefficient of static friction between the box and the train's floor is 0.2. The maximum acceleration of the train in which a box lying on its floor will remain stationary is (Take g = 10 ms−2)
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5ms−2. The frictional force acting on the block is then
A block of mass 2kg rest on a plane inclined at an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is 0.7. What will be the frictional force acting on the block?
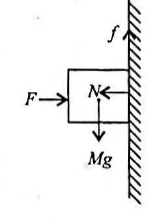
A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is μ and the acceleration due to gravity is g, what is the minimum force required to be applied by the finger to hold the block against the wall?
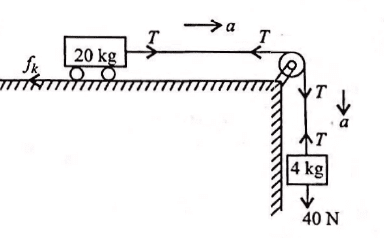
A trolley of mass 20kg is attached to a block of mass 4kg by a massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the acceleration of the trolley and block system is(Take g = 10ms−2)
|
237 docs|243 tests
|



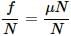 or
or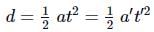 (∵ u = 0)
(∵ u = 0)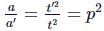 (∵ t′ = 20ps,t=20s)
(∵ t′ = 20ps,t=20s)  (Using (i) and (ii))
(Using (i) and (ii))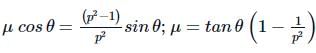 Here, θ=30∘ ∴ μ =
Here, θ=30∘ ∴ μ =