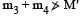Test: Comprehension Based: Modern Physics | JEE Main - JEE MCQ
17 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: Comprehension Based: Modern Physics | JEE Main
PASSAGE - 1
In a mixture of H-He+ gas (He+ is singly ionized He atom), H atoms and He+ ions are excited to their respective first excited states. Subsequently, H atoms transfer their total excitation energy to He+ ions (by collisions). Assume that the Bohr model of atom is exactly valid.
Q. The quantum number n of the state finally populated in He+ ions is –
PASSAGE - 1
In a mixture of H-He+ gas (He+ is singly ionized He atom), H atoms and He+ ions are excited to their respective first excited states. Subsequently, H atoms transfer their total excitation energy to He+ ions (by collisions). Assume that the Bohr model of atom is exactly valid.
Q. The wavelength of light emitted in the visible region by He+ ions after collisions with H atoms is –
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
PASSAGE - 1
In a mixture of H-He+ gas (He+ is singly ionized He atom), H atoms and He+ ions are excited to their respective first excited states. Subsequently, H atoms transfer their total excitation energy to He+ ions (by collisions). Assume that the Bohr model of atom is exactly valid.
Q. The ratio of the kinetic energy of the n = 2 electron for the H atom to that of He+ ion is –
PASSAGE-2
Scientists are working hard to develop nuclear fusion reactor.
Nuclei of heavy hydrogen, 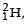 known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is
known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is 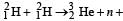 energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of
energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of 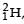 nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
Special techniques are used which confine the plasma for a time t0 before the particles fly away form the core. If n is the density (number/volume) of deuterons, the product nt0 is called Lawson number. In one of the criteria, a reactor is termed successful if Lawson number is greater than 5 × 1014 s/cm3.
It may be helpful to use the following: Boltzmann constant 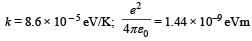
Q. In the core of nuclear fusion reactor, the gas becomes plasma because of
PASSAGE-2
Scientists are working hard to develop nuclear fusion reactor.
Nuclei of heavy hydrogen, 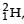 known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is
known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is 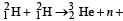 energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of
energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of 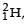 nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
Special techniques are used which confine the plasma for a time t0 before the particles fly away form the core. If n is the density (number/volume) of deuterons, the product nt0 is called Lawson number. In one of the criteria, a reactor is termed successful if Lawson number is greater than 5 × 1014 s/cm3.
It may be helpful to use the following: Boltzmann constant 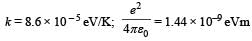
Q. Assume that two deuteron nuclei in the core of fusion reactor at temperature T are moving towards each other, each with kinetic energy 1.5 kT, when the separation between them is large enough to neglect coulomb potential energy. Also neglect any interaction from other particles in the core. The minimum temperature T required for them to reach a separation of 4 × 10–15 m is in the range
PASSAGE-2
Scientists are working hard to develop nuclear fusion reactor.
Nuclei of heavy hydrogen, 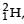 known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is
known as deuteron and denoted by D, can be thought of as a candidate for fusion reactor. The D-D r eaction is 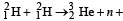 energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of
energy. In the core of fusion reactor, a gas of heavy hydrogen is fully ionized into deuteron nuclei and electrons. This collection of 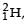 nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
nuclei and electrons is known as plasma. The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually, the temperatures in the reactor core are too high and no material wall can be used to confine the plasma.
Special techniques are used which confine the plasma for a time t0 before the particles fly away form the core. If n is the density (number/volume) of deuterons, the product nt0 is called Lawson number. In one of the criteria, a reactor is termed successful if Lawson number is greater than 5 × 1014 s/cm3.
It may be helpful to use the following: Boltzmann constant 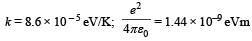
Q. Results of calculations for four different designs of a fusion reactor using D-D reaction are given below. Which of these is most promising based on Lawson criterion?
PASSAGE-3
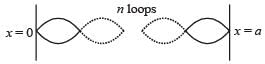
When a particle is restricted to move along x - axis between x = 0 and x = a, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x = 0 and x = a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as 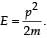 Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving in the line x = 0 to x = a. Take h = 6.6 × 10–34 J s and e = 1.6 × 10–19 C.
Q. The allowed energy for the particle for a particular value of n is proportional to
PASSAGE-3
When a particle is restricted to move along x - axis between x = 0 and x = a, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x = 0 and x = a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as 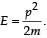 Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving in the line x = 0 to x = a. Take h = 6.6 × 10–34 J s and e = 1.6 × 10–19 C.
Q. If the mass of the particle is m = 1.0 × 10–30 kg and a = 6.6 nm, the energy of the particle in its ground state is closest to
PASSAGE-3
When a particle is restricted to move along x - axis between x = 0 and x = a, where a is of nanometer dimension, its energy can take only certain specific values. The allowed energies of the particle moving in such a restricted region, correspond to the formation of standing waves with nodes at its ends x = 0 and x = a . The wavelength of this standing wave is related to the linear momentum p of the particle according to the de Broglie relation. The energy of the particle of mass m is related to its linear momentum as 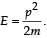 Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Thus, the energy of the particle can be denoted by a quantum number ‘n’ taking values1, 2, 3, ... (n = 1, called the ground state) corresponding to the number of loops in the standing wave.
Use the model described above to answer the following three questions for a particle moving in the line x = 0 to x = a. Take h = 6.6 × 10–34 J s and e = 1.6 × 10–19 C.
Q. The speed of the particle, that can take discrete values, is proportional to
PASSAGE - 4
The key feature of Bohr’s theory of spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid. The rule to be applied is Bohr ’s quantization condition.
Q. A diatomic molecule has moment of inertia I. By Bohr ’s quantization condition its rotational energy in the nth level (n = 0 is not allowed) is
PASSAGE - 4
The key feature of Bohr’s theory of spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid. The rule to be applied is Bohr ’s quantization condition.
Q. It is found that the excitation frequency from ground to the first excited state of rotation for the CO molecule is close 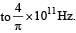 Then the moment of inertia of CO molecule about its center of mass is close to
Then the moment of inertia of CO molecule about its center of mass is close to
(Take h = 2π × 10 –34 J s)
PASSAGE - 4
The key feature of Bohr’s theory of spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid. The rule to be applied is Bohr ’s quantization condition.
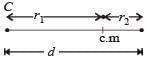
Q. In a CO molecule, the distance between C (mass = 12 a.m.u.) and O (mass = 16 a.m.u.), where 1 a.m.u. 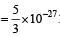 kg, is close to
kg, is close to
PASSAGE - 5
The β -decay process, discovered around 1900, is basically the decay of a neutron (n). In the laboratory, a proton (p) and an electron (e–) are observed as the decay products of the neutron.
Therefore, considering the decay of a neutron as a two-body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant. But experimentally, it was observed that the electron kinetic energy has continuous spectrum. Considering a three-body decay process, i.e. 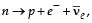 around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino
around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino 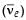 to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8 × 106 eV. The kinetic energy carried by the proton is only the recoil energy.
to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8 × 106 eV. The kinetic energy carried by the proton is only the recoil energy.
Q. If the anti-neutrino had a mass of 3 eV/c2 (where c is the speed of light) instead of zero mass, what should be the range of the kinetic energy, K, of the electron?
PASSAGE - 5
The β -decay process, discovered around 1900, is basically the decay of a neutron (n). In the laboratory, a proton (p) and an electron (e–) are observed as the decay products of the neutron.
Therefore, considering the decay of a neutron as a two-body decay process, it was predicted theoretically that the kinetic energy of the electron should be a constant. But experimentally, it was observed that the electron kinetic energy has continuous spectrum. Considering a three-body decay process, i.e. 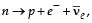 around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino
around 1930, Pauli explained the observed electron energy spectrum. Assuming the anti-neutrino 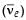 to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8 × 106 eV. The kinetic energy carried by the proton is only the recoil energy.
to be massless and possessing negligible energy, and the neutron to be at rest, momentum and energy conservation principles are applied. From this calculation, the maximum kinetic energy of the electron is 0.8 × 106 eV. The kinetic energy carried by the proton is only the recoil energy.
Q. What is the maximum energy of the anti-neutrino?
PASSAGE - 6
The mass of a nucleus 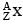 is less than the sum of the masses of (A-Z) number of neutrons and Z number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses m1 and m2 only if (m1 + m2) < M. Also two light nuclei of masses m3 and m4 can undergo complete fusion and form a heavy nucleus of mass M' only if (m3 + m4) > M'. The masses of some neutral atoms are given in the table below:
is less than the sum of the masses of (A-Z) number of neutrons and Z number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses m1 and m2 only if (m1 + m2) < M. Also two light nuclei of masses m3 and m4 can undergo complete fusion and form a heavy nucleus of mass M' only if (m3 + m4) > M'. The masses of some neutral atoms are given in the table below:
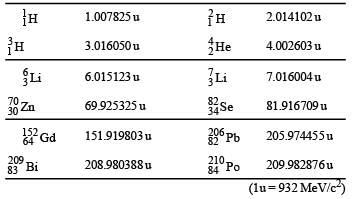
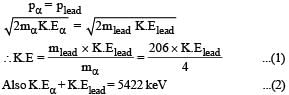
Q. The kinetic energy (in keV) of the alpha particle, when the nucleus 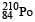 at rest undergoes alpha decay, is
at rest undergoes alpha decay, is
PASSAGE - 6
The mass of a nucleus 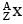 is less than the sum of the masses of (A-Z) number of neutrons and Z number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses m1 and m2 only if (m1 + m2) < M. Also two light nuclei of masses m3 and m4 can undergo complete fusion and form a heavy nucleus of mass M' only if (m3 + m4) > M'. The masses of some neutral atoms are given in the table below:
is less than the sum of the masses of (A-Z) number of neutrons and Z number of protons in the nucleus. The energy equivalent to the corresponding mass difference is known as the binding energy of the nucleus. A heavy nucleus of mass M can break into two light nuclei of masses m1 and m2 only if (m1 + m2) < M. Also two light nuclei of masses m3 and m4 can undergo complete fusion and form a heavy nucleus of mass M' only if (m3 + m4) > M'. The masses of some neutral atoms are given in the table below:
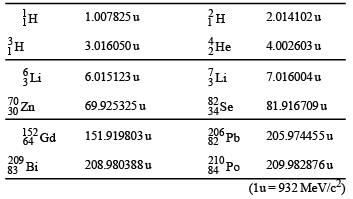
Q. The correct statement is
STATEMENT-1 If the accelerating potential in an X-ray tube is increased, the wavelengths of the characteristic X-rays do not change.
STATEMENT-2 When an electron beam strikes the target in an X-ray tube, part of the kinetic energy is converted into X-ray energy.
|
347 docs|185 tests
|
|
347 docs|185 tests
|


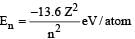
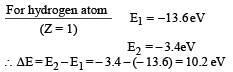
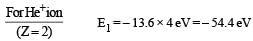
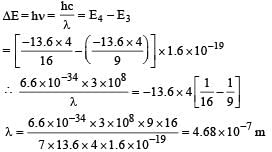
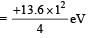
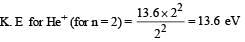
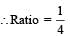
 nuclei and electron is known as plasma which is formed due to high temperature inside the reactor core.
nuclei and electron is known as plasma which is formed due to high temperature inside the reactor core.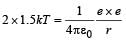
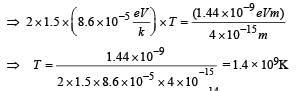
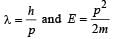
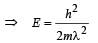
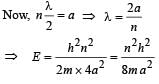
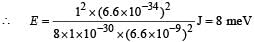
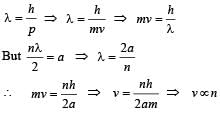
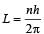
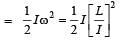
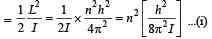
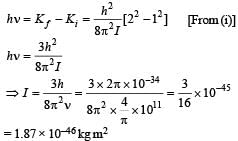
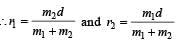
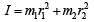
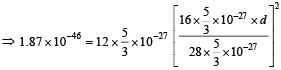
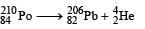
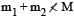 and in the other case of fusion
and in the other case of fusion