Test: Congruence Criteria- SAS And ASA
15 Questions MCQ Test Mathematics (Maths) Class 9 | Test: Congruence Criteria- SAS And ASA
| 1 Crore+ students have signed up on EduRev. Have you? |
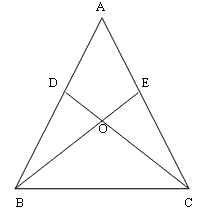
In the given figure, AB = AC, AD = AE = 5 cm and DC = 8 cm. Length of EB is______.
8 cm is the answer because DC = EB = 8 cm.
Triangle ABC is congruent to triangle DEF. Which side is congruent to side BC?
The side BC is congruent to side EF.
Which of the following statements is incorrect ?
2 rectangles having same area may differ in their lengths. So they will not be congruent
In the following figure, PQ = PR and SQ = SR, then
In △PQR and △SRQ,
► PQ = SR(Given)
► QR = QR(Common)
► PR = SQ(Given)
By SSS property:
△PQR≅△SRQ
Therefore, ∠PQS =∠PRS
If two triangles ABC and PQR are congruent under the correspondence A ↔ P, B ↔ Q and C ↔ R, then symbolically, it is expressed as
If ΔABC ≌ ΔPQR then, which of the following is true?
Corresponding sides in congruent triangles are equal.
So AC = PR ,AB = PQ ,BC = QR
If two sides of a triangle are equal, the angles opposite to these sides are______.
Theorem: Angles opposite to equal sides of an isosceles triangle are equal.
In case of two equilateral triangles, PQR and STU which of the following correspondence is not correct?
The correct option is Option A.
All equilateral triangles have the same angles by the congruence rule (SSS)
So, TTS <—> PQR
In quadrilateral ADBC, AB bisects ∠A. Which of the following criterion will prove ΔABC ≅ ΔABD?
In quadrilateral ADBC we have:
► AC = AD
and AB being the bisector of ∠A.
Now, in ΔABC and ΔABD:
► AC = AD [Given]
► AB = AB [Common]
► ∠CAB = ∠DAB [∴ AB bisects ∠CAD]
∴ Using SAS criteria, we have
ΔABC ≌ ΔABD.
∴ Corresponding parts of congruent triangles (c.p.c.t) are equal.
∴ BC = BD
In an isosceles triangle ABC with AB = AC, if BD and CE are the altitudes, then BD and CE are______.
Given: △ABC, AB=AC, BD⊥AC and CE⊥AB
Area of triangle = 1/2 × base × height
Area of △ABC = 1/2 × AB × CE = 1/2 × BD × AC
CE = BD (Since, AB=AC)
In fig., if AB = AC and PB = QC, then by which congruence criterion PBC ≅ QCB
As AB = AC so angle ACB = angle(ABC) as angles opposite to equal sides r equal.
In triangle PBC and Triangle QCB we see that:
i) PB = QC (given)
ii) angle(PBC) = (angle)QCB (proved earliar)
iii) BC = BC (common)
So, triangle PBC is congruent to triangle QCB by SAS axiom of congruency.
The diagonal PR of a quadrilateral PQRS bisects the angles P and R, then
In Δ PSR and ΔPQR
► PR = PR
► ∠ 1 = ∠ 2
► ∠ 3 = ∠ 4
Δ PSR ≅ Δ PQR [ASA]
► PS = PQ [CPCT]
► QR = RS [CPCT]
The correct option is Option A
In the given figure, AB = EF, BC = DE, AB ⊥ BD and EF ⊥ CE. Which of the following criterion is true for ΔABD ≅ ΔEFC?
In triangle ABD and FEC:
► AB = FE ( given )
► ∠FEC = ∠ABD ( 90degree)
► BC = DE
CD is common part coming in both triangles.
► BC + CD = CD + DE
► BD = CE
Therefore, triangle ABD is congruent to triangle FEC by SAS rule of congruence.
Two figures are congruent if they have______.
In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
The least number of acute angles that a triangle can have is 2.
As we cannot have more than one right angle or obtuse angle, we have only two or three acute angles in a triangle.
Further, if one angle is acute, sum of other two angles is more than 900 and we cannot have two right angles or obtuse angles.
|
84 videos|352 docs|109 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
84 videos|352 docs|109 tests
|
Download free EduRev App
Related content with Test: Congruence Criteria- SAS And ASA
|
|
|
Related tests with Test: Congruence Criteria- SAS And ASA
|
|
|
|
|
|
© EduRev
|
Follow Us
|